原文献：http://distill.pub/2021/gnn-intro/

图卷积介绍

神经网络已经被调整以利用图的结构和属性。我们探讨了构建图神经网络所需的组件，并解释了它们背后的设计选择动机。

AUTHORS AFFILIATIONS

Benjamin Sanchez-Lengeling Google Research

Emily Reif Google Research

Adam Pearce Google Research

Alexander B. Wiltschko Google Research

PUBLISHED Sept. 2, 2021

DOI 10.23915/distill.00033

这篇文章是《Distill》关于图神经网络的两篇出版物之一。请查看《理解图上的卷积》[1]，以了解如何将图上的卷积自然地推广到图上的卷积。

图形无处不在；现实世界中的物体通常是通过与其他事物的连接来定义的。一组对象及其之间的连接可以自然地表示为一个图。研究人员在过去十多年中开发了在图数据上运行的神经网络（称为图神经网络或GNNs）[2]。最近的发展提升了它们的能力和表达能力。我们开始在抗菌药物发现[3]、物理模拟[4]、假新闻检测[5]、交通预测[6]和推荐系统[7]等领域看到实际应用。

本文探讨并解释了现代图神经网络。我们将这项工作分为四个部分。首先，我们看看哪种类型的数据最自然地表达为一个图，以及一些常见的例子。其次，我们探讨了图与其他类型的数据的区别，以及在使用图时需要做出的一些专门选择。第三，我们构建一个现代的GNN，逐步介绍模型的各个部分，从该领域的历史建模创新开始。我们从一个最基本的实现逐渐过渡到一个最先进的GNN模型。第四，最后，我们提供了一个GNN游乐场，您可以在其中玩耍一个真实世界的任务和数据集，以更好地理解GNN模型的每个组件如何影响其所做的预测。

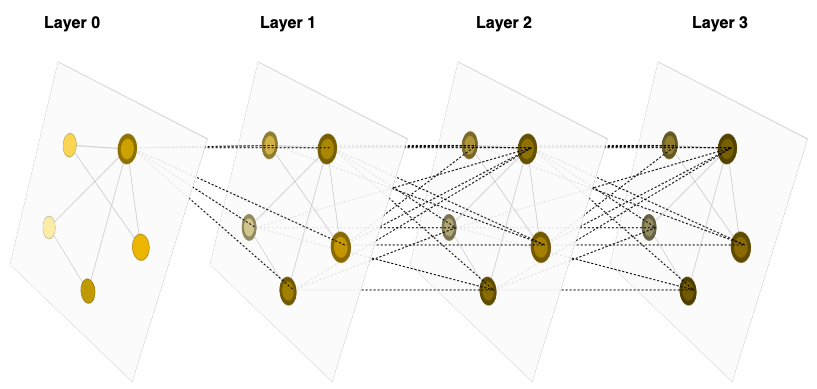
首先，让我们确定什么是一个图。一个图表示了一组实体（节点）之间的关系（边）。

为了进一步描述每个节点、边或整个图，我们可以在图的每个部分中存储信息。

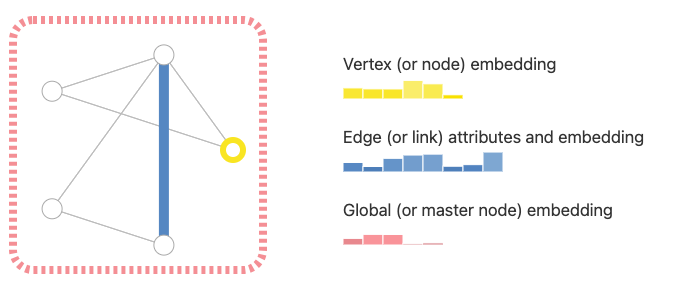
此外，我们可以通过将方向性与边关联（有向的、无向的）来进一步特殊化图形。

边可以是有向的，其中边 𝑒 有一个源节点 𝑣_{𝑠𝑟𝑐} 和一个目标节点 𝑣_{𝑑𝑠𝑡}。在这种情况下，信息从 𝑣_{𝑠𝑟𝑐} 流向 𝑣_{𝑑𝑠𝑡}。它们也可以是无向的，其中没有源节点或目标节点的概念，信息在两个方向上都流动。请注意，拥有一个单独的无向边等效于具有一条从 𝑣_{𝑠𝑟𝑐} 到 𝑣_{𝑑𝑠𝑡} 的有向边，以及另一条从 𝑣_{𝑑𝑠𝑡}到 𝑣_{𝑠𝑟𝑐} 的有向边。

图是非常灵活的数据结构，如果现在看起来抽象，我们将在下一节通过例子来具体说明。

图及其应用领域

你可能已经熟悉了一些类型的图数据，比如社交网络。然而，图是一种非常强大且通用的数据表示方式，我们将展示两种你可能没有想到可以建模为图的数据类型：图像和文本。虽然有些令人费解，但通过将它们视为图形来学习图像和文本的对称性和结构，可以建立直观的理解，从而帮助理解其他不那么网格状的图数据，我们将在后面讨论。

图像作为图表达

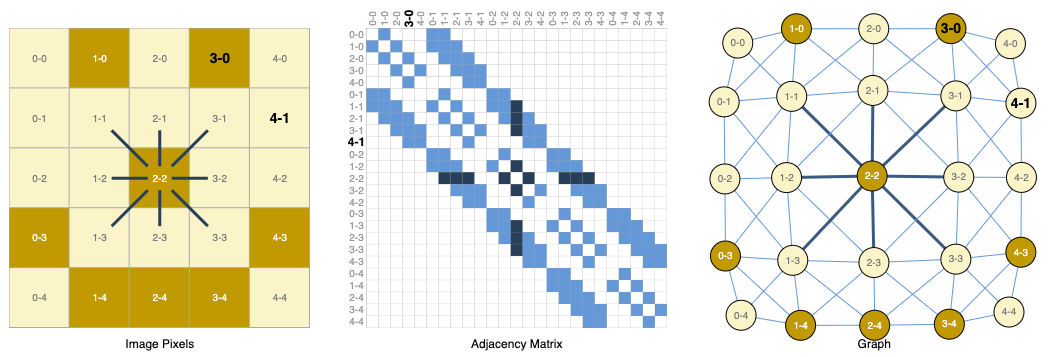
通常我们会将图像看作是具有图像通道的矩形网格，将其表示为数组（例如，244x244x3 的浮点数数组）。另一种思考图像的方式是将其视为具有规则结构的图，其中每个像素表示一个节点，并通过边与相邻像素相连。每个非边缘像素恰好有8个邻居，而每个节点存储的信息是一个三维向量，表示像素的RGB值。

通过邻接矩阵是一种可视化图的连接方式。我们对节点进行排序，例如在一个简单的 5×5 微笑脸图像中有 25 个像素点，然后填充一个大小为 𝑛_{𝑛𝑜𝑑𝑒𝑠}× 𝑛_{𝑛𝑜𝑑𝑒𝑠} 的矩阵，如果两个节点共享一条边，则在相应的位置填入一个条目。请注意，以下这三种表达方式实际上是同一组数据的不同视图。

文字作为图表达

我们可以通过为每个字符、单词或标记分配索引，并将文本表示为这些索引的序列来数字化文本。这样创建了一个简单的有向图，其中每个字符或索引是一个节点，并通过一条边连接到其后面的节点。

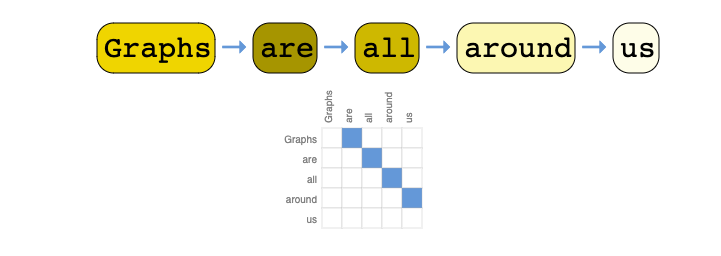
当然，在实践中，通常不会以这种方式对文本和图像进行编码：这些图形表示是冗余的，因为所有图像和所有文本都具有非常规则的结构。例如，图像在其邻接矩阵中具有带状结构，因为所有节点（像素）都在网格中相互连接。文本的邻接矩阵只是一条对角线，因为每个单词只与前一个单词和后一个单词相连。

这种表示方式（字符标记的序列）指的是文本在循环神经网络（RNNs）中通常的表示方式；其他模型，比如变压器（Transformers），可以被看作是将文本视为一个完全连接的图，我们在其中学习标记之间的关系。更多信息请参阅《图注意力网络》（Graph Attention Networks）。

自然界中的图

图是描述你可能已经熟悉的数据的有用工具。让我们继续讨论结构更加异构的数据。在这些例子中，每个节点的邻居数量是可变的（与图像和文本的固定邻域大小相对）。除了以图的方式表达之外，很难用任何其他方式表达这种数据。

分子作为图形：

分子是物质的基本组成单位，由三维空间中的原子和电子构成。所有粒子都在相互作用，但当一对原子被固定在彼此稳定的距离时，我们称它们共用一个共价键。不同的原子对和键具有不同的距离（例如单键、双键）。将这个三维对象描述为一个图形是一个非常方便和常见的抽象，其中节点是原子，边是共价键。[8]以下是两种常见分子及其关联的图形。

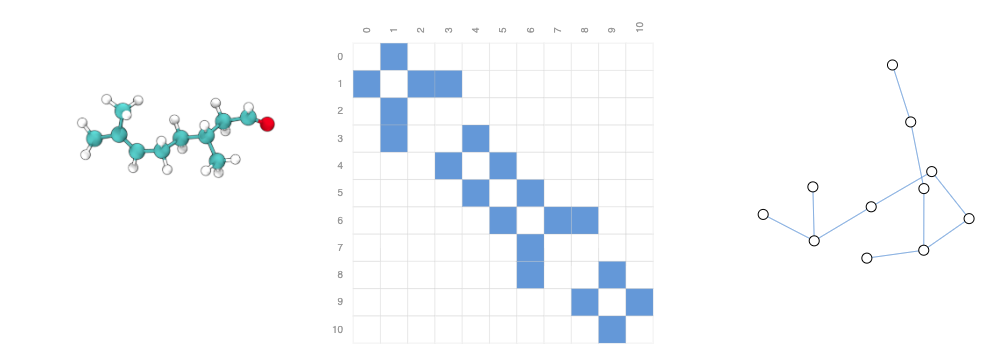
（左）柠檬香醛分子的三维表示（中）该分子中键的邻接矩阵（右）分子的图形表示。

(左) 咖啡因分子的三维表示（中）该分子中键的邻接矩阵（右）分子的图形表示。

社交网络作为图：

社交网络是研究人员、机构和组织集体行为模式的工具。我们可以通过将个体建模为节点，将它们之间的关系建模为边，来构建代表人群的图形。

（左）来自戏剧《奥赛罗》的场景图像。（中）该剧中角色之间互动的邻接矩阵。（右）这些互动的图形表示。

与图像和文本数据不同，社交网络的邻接矩阵并不相同。

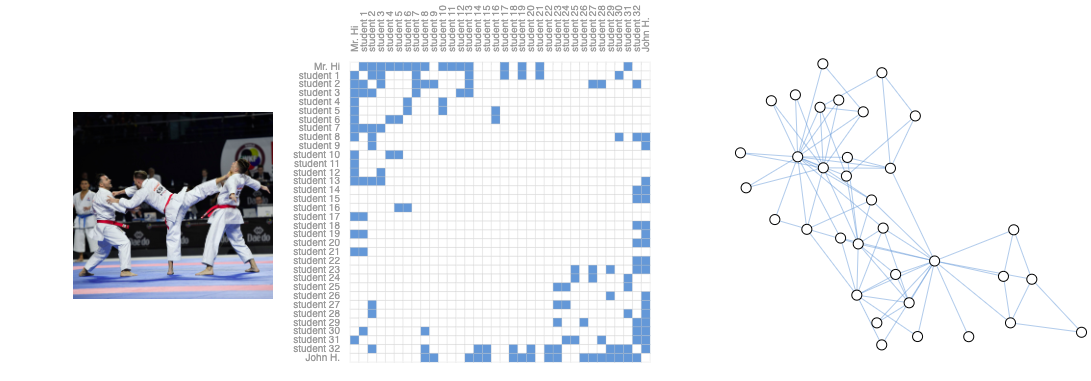
(左) 空手道比赛的图像。（中）空手道俱乐部成员之间互动的邻接矩阵。（右）这些互动的图形表示。

引用网络作为图 ：

科学家在发表论文时通常会引用其他科学家的工作。我们可以将这些引用网络可视化为一个图形，其中每篇论文是一个节点，每条有向边表示一篇论文对另一篇论文的引用。此外，我们还可以将有关每篇论文的信息添加到每个节点中，例如摘要的词嵌入（参见[9]，[10]，[11]）。

其他例子:

在计算机视觉中，我们有时想要在视觉场景中标记物体。我们可以将这些物体视为节点，将它们之间的关系视为边来构建图形。机器学习模型、编程代码[12]和数学方程[13]也可以被看作是图形，其中变量是节点，而边是将这些变量作为输入和输出的操作。你可能会在某些上下文中看到术语“数据流图”的使用。

数据集	领域	图量	节点数	边数	最小度	平均度	最大度
karate club	Social network	1	34	78		4.5	17
qm9	Small molecules	134k	<=9	<=26	1	2	5
Cora	Citation network	1	23166	91500	1	7.8	379
Wikipedia links, English	Knowledge graph	1	12M	378M		62.24	1M

实际世界中发现的图形的摘要统计数据。这些数字取决于特征化决策。可以在KONECT中找到更多有用的统计数据和图形。

哪些问题涉及到图结构化数据？

我们已经描述了一些现实世界中的图形示例，但我们想要对这些数据执行哪些任务呢？关于图形的预测任务通常可以分为三类：图级别、节点级别和边级别。

在图级别任务中，我们预测整个图的单一属性。在节点级别任务中，我们预测图中每个节点的某些属性。在边级别任务中，我们希望预测图中边的属性或存在与否。

对于上述三个级别的预测问题（图级别、节点级别和边级别），我们将展示所有以下问题都可以使用单一模型类别，即GNN来解决。但首先，让我们更详细地了解这三类图形预测问题，并提供每个问题的具体示例。

还有其他相关的任务是活跃研究领域。例如，我们可能想要生成图形，或者解释对图形的预测结果。更多的主题可以在“深入细节”部分找到。

图级别任务

在图级别任务中，我们的目标是预测整个图的某种属性。例如，对于一个以图形表示的分子，我们可能想要预测这个分子的气味，或者它是否会与与一种与疾病相关的受体结合。

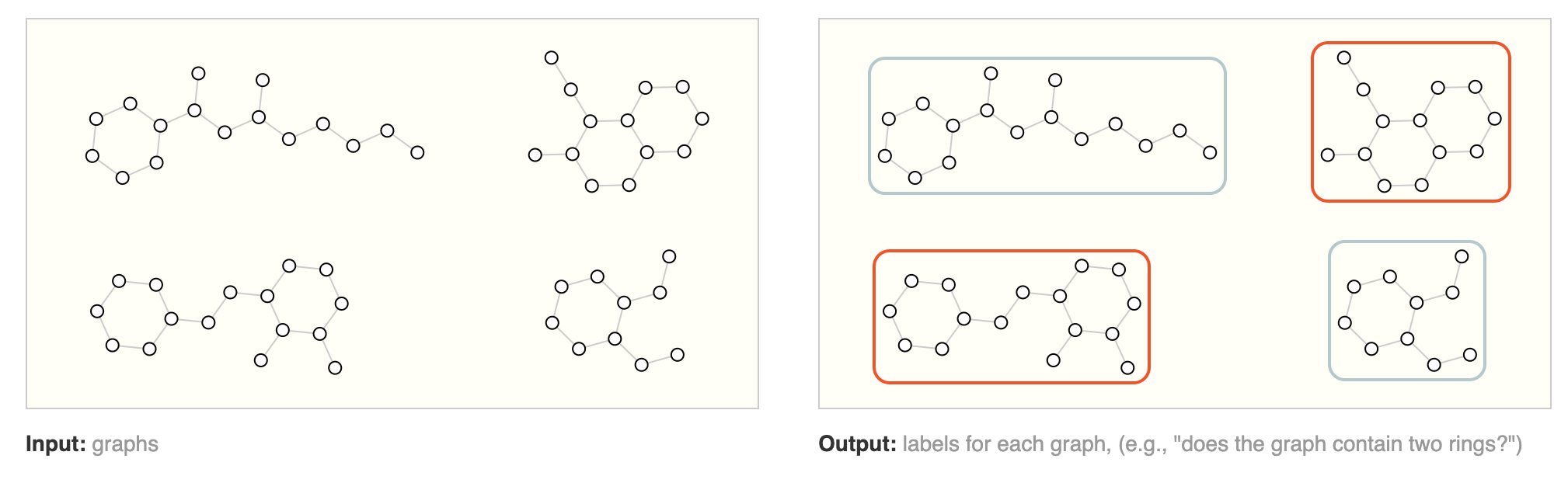
这类似于MNIST和CIFAR等图像分类问题，其中我们想要为整个图像关联一个标签。在文本方面，类似的问题是情感分析，我们希望一次性识别一整个句子的情感或情绪。

节点级别任务

节点级别任务涉及在图中预测每个节点的身份或角色。

一个经典的节点级别预测问题的例子是扎克的空手道俱乐部[15]。该数据集是一个单一的社交网络图，由在政治纷争后宣誓效忠两个空手道俱乐部之一的个人组成。故事如下，Mr. Hi（教练）和John H（管理员）之间的纷争在空手道俱乐部中造成了分裂。节点代表个体空手道练习者，边代表这些成员在空手道以外的领域之间的互动。预测问题是在纷争后，预测给定成员是否会忠诚于Mr. Hi或John H。在这种情况下，节点到教练或管理员的距离与该标签高度相关。

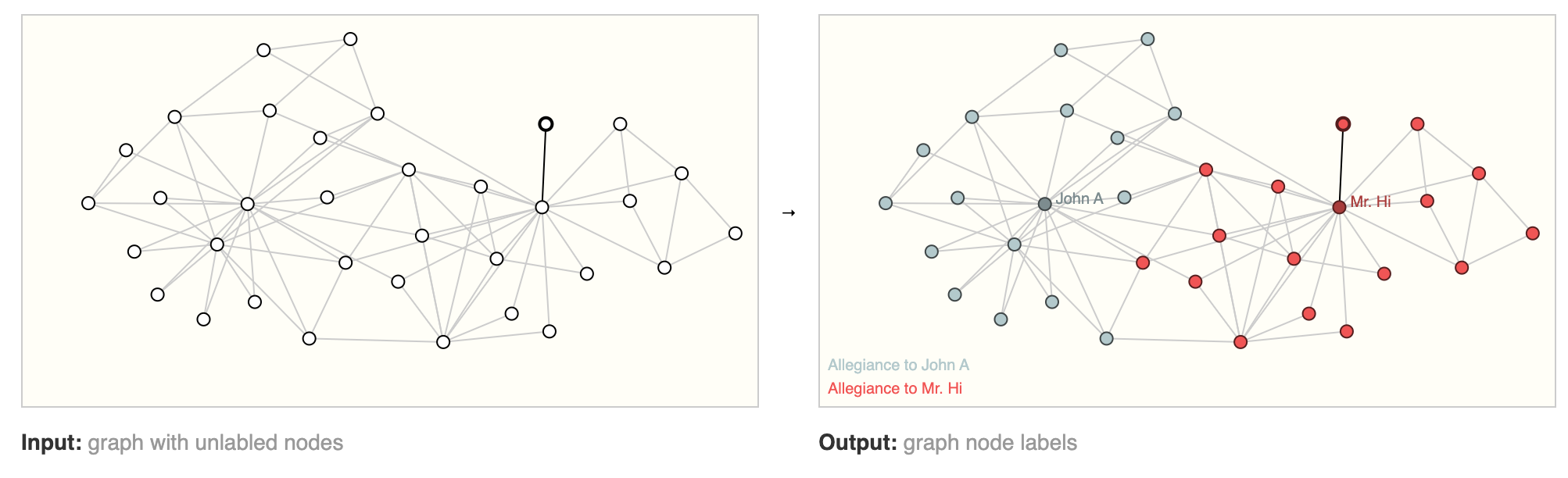
在左侧，我们有问题的初始条件，在右侧，我们有一个可能的解决方案，其中每个节点根据其所属联盟进行了分类。该数据集可以在其他图问题中使用，如无监督学习。

类比图像，节点级别预测问题类似于图像分割，我们试图为图像中的每个像素贴上标签。在文本方面，类似的任务是预测句子中每个单词的词性（如名词、动词、副词等）。

边级别任务

在图形中剩下的预测问题是边级别的预测。

边级别推断的一个例子是图像场景理解。除了在图像中识别对象外，深度学习模型可以用于预测它们之间的关系。我们可以将这视为边级别的分类问题：在给定代表图像中的对象的节点的情况下，我们希望预测这些节点中哪些共享一条边，或者这条边的值是什么。如果我们希望发现实体之间的连接，我们可以将图形视为完全连接的，并根据它们的预测值修剪边缘以得到稀疏的图形。

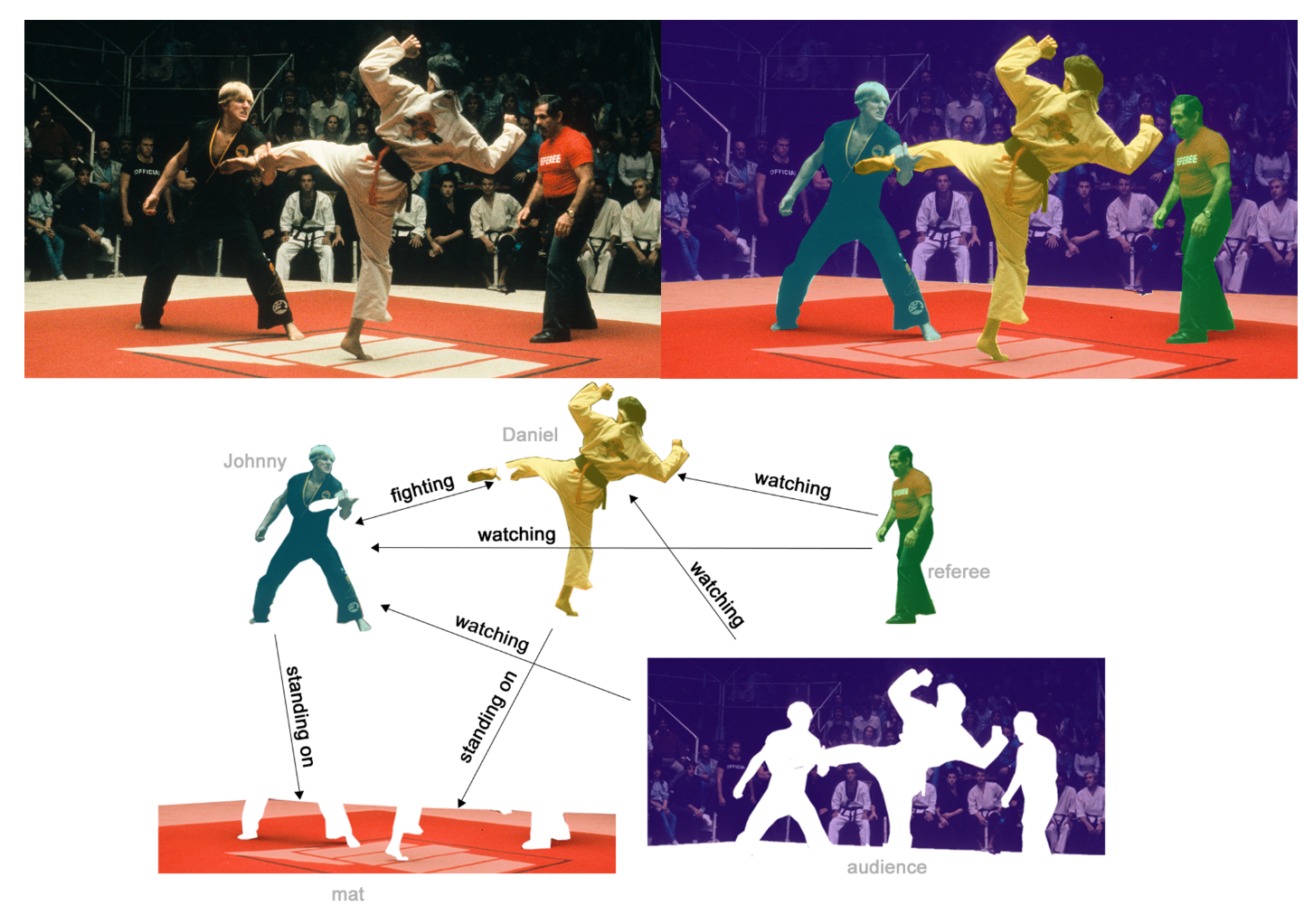
在上图的(b)部分中，原始图像(a)已经被分割成了五个实体：每个斗士、裁判、观众和地垫。而(c)展示了这些实体之间的关系。

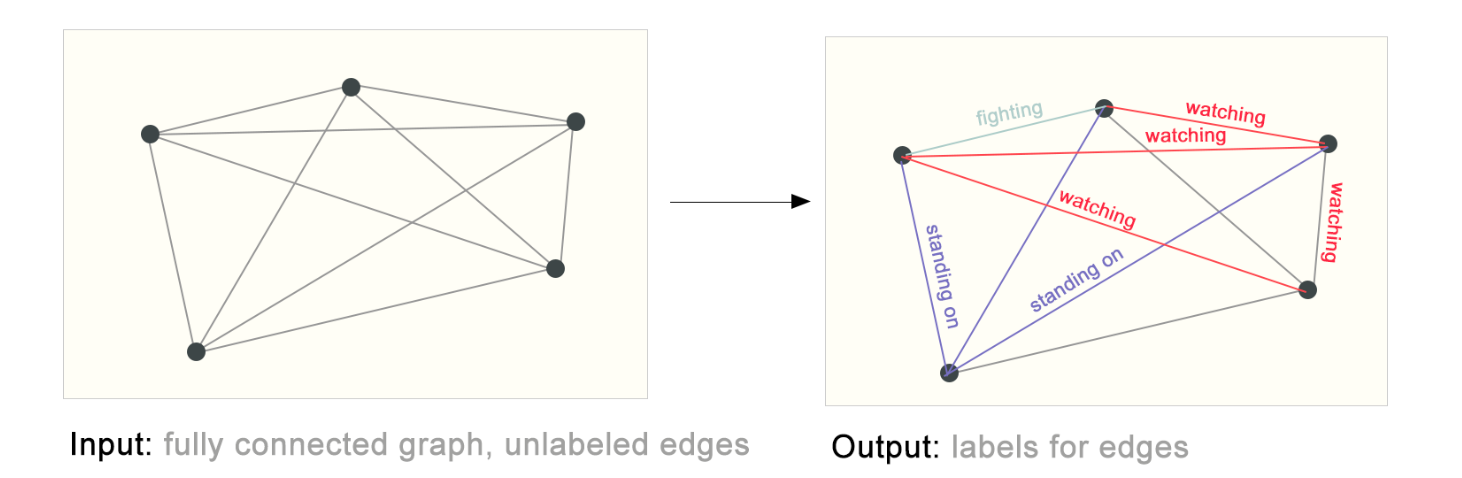
在左侧，我们有一个从之前的视觉场景构建的初始图形。在右侧是该图形的一个可能的边标签，当一些连接基于模型的输出被剪除时。

在机器学习中使用图形所面临的挑战

那么，我们如何用神经网络解决这些不同的图任务呢？第一步是考虑如何表示图，以使其与神经网络兼容。

机器学习模型通常将矩形或类似网格的数组作为输入。因此，如何以与深度学习兼容的格式表示它们并不是立即直观的。图形具有多达四种类型的信息，我们可能希望用来进行预测：节点、边、全局上下文和连接性。前三者相对简单：例如，对于节点，我们可以通过为每个节点分配一个索引 𝑖 并将 𝑛𝑜𝑑𝑒_𝑖 的特征存储在 𝑁 中来形成一个节点特征矩阵 𝑁。虽然这些矩阵具有可变数量的示例，但它们可以在不需要任何特殊技巧的情况下进行处理。

然而，表示图的连接性就比较复杂了。也许最明显的选择是使用邻接矩阵，因为这很容易转化为张量。然而，这种表示方法有一些缺点。从示例数据集表格中，我们可以看到图中的节点数量可能达到百万级，每个节点的边数可能会变化很大。通常，这会导致非常稀疏的邻接矩阵，这在空间上效率低下。

另一个问题是有许多邻接矩阵可以编码相同的连接性，并且不能保证这些不同的矩阵在深度神经网络中会产生相同的结果（也就是说，它们不是置换不变的）。

例如，之前提到的《奥赛罗》图可以用这两个邻接矩阵等效地描述。它还可以用节点的每一种可能的置换来描述。

两个表示同一图的邻接矩阵。

下面的示例显示了可以描述这个包含4个节点的小图的每个邻接矩阵。这已经是相当大量的邻接矩阵了，对于像《奥赛罗》这样更大的示例，这个数量是难以处理的。

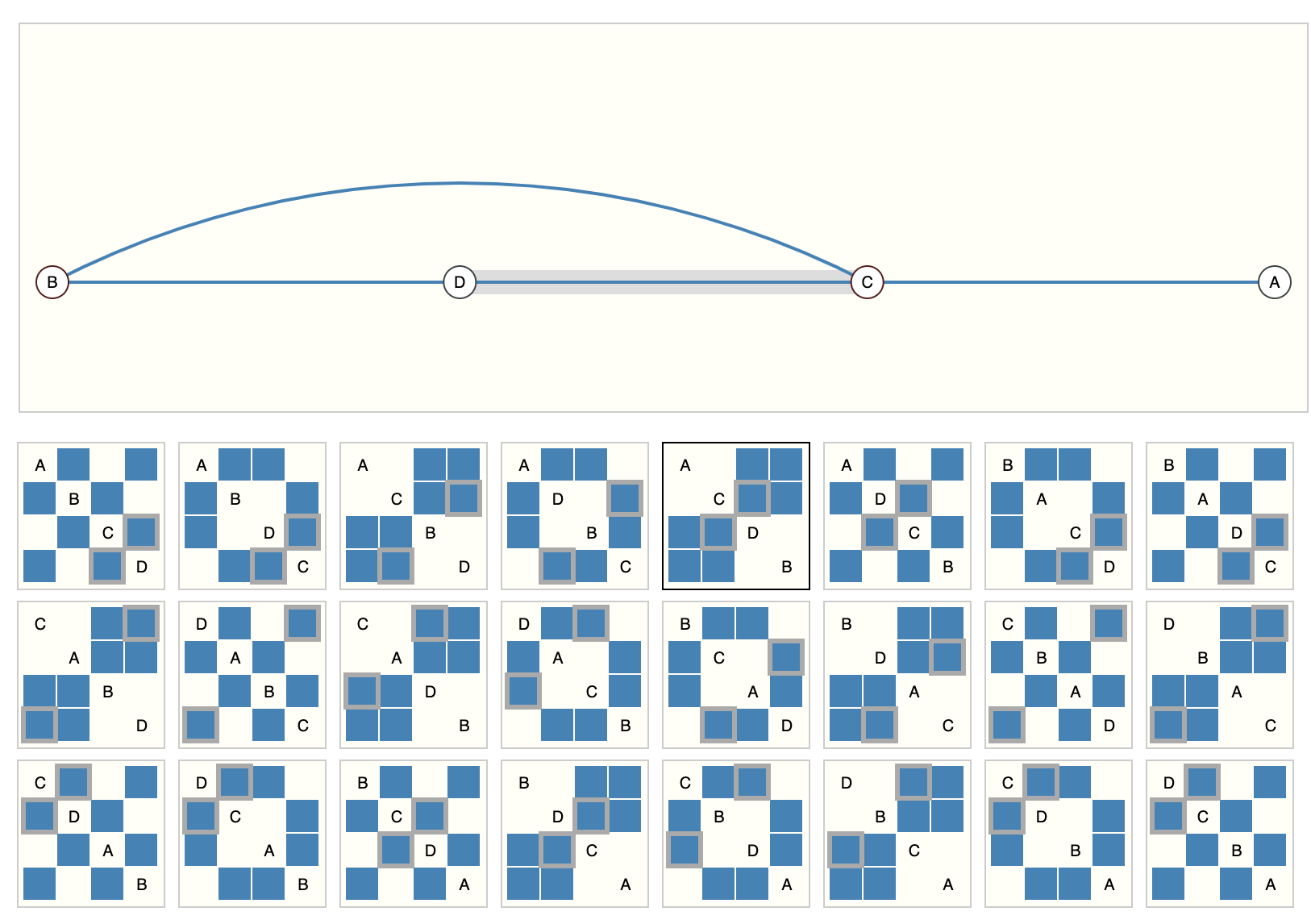
所有这些邻接矩阵代表同一个图。点击一条边以移除它，点击“虚拟边”以添加它，矩阵将相应地更新。

一种优雅且内存高效的稀疏矩阵表示方法是邻接表。它们将边 𝑒_𝑘 在节点 𝑛_𝑖 和 𝑛_𝑗 之间的连接性描述为邻接表的第 k 个条目中的元组 (i,j)。由于我们预期边的数量远远低于邻接矩阵的条目数（𝑛^2_{𝑛𝑜𝑑𝑒𝑠}），我们避免了在图的未连接部分进行计算和存储。

另一种陈述这一点的方式是使用大O符号表示，最好是具有O(𝑛_{𝑒𝑑𝑔𝑒𝑠})的复杂度，而不是O(𝑛^2_{𝑛𝑜𝑑𝑒𝑠})。

为了使这个概念具体化，我们可以看看在这种规范下如何表示不同图的信息：

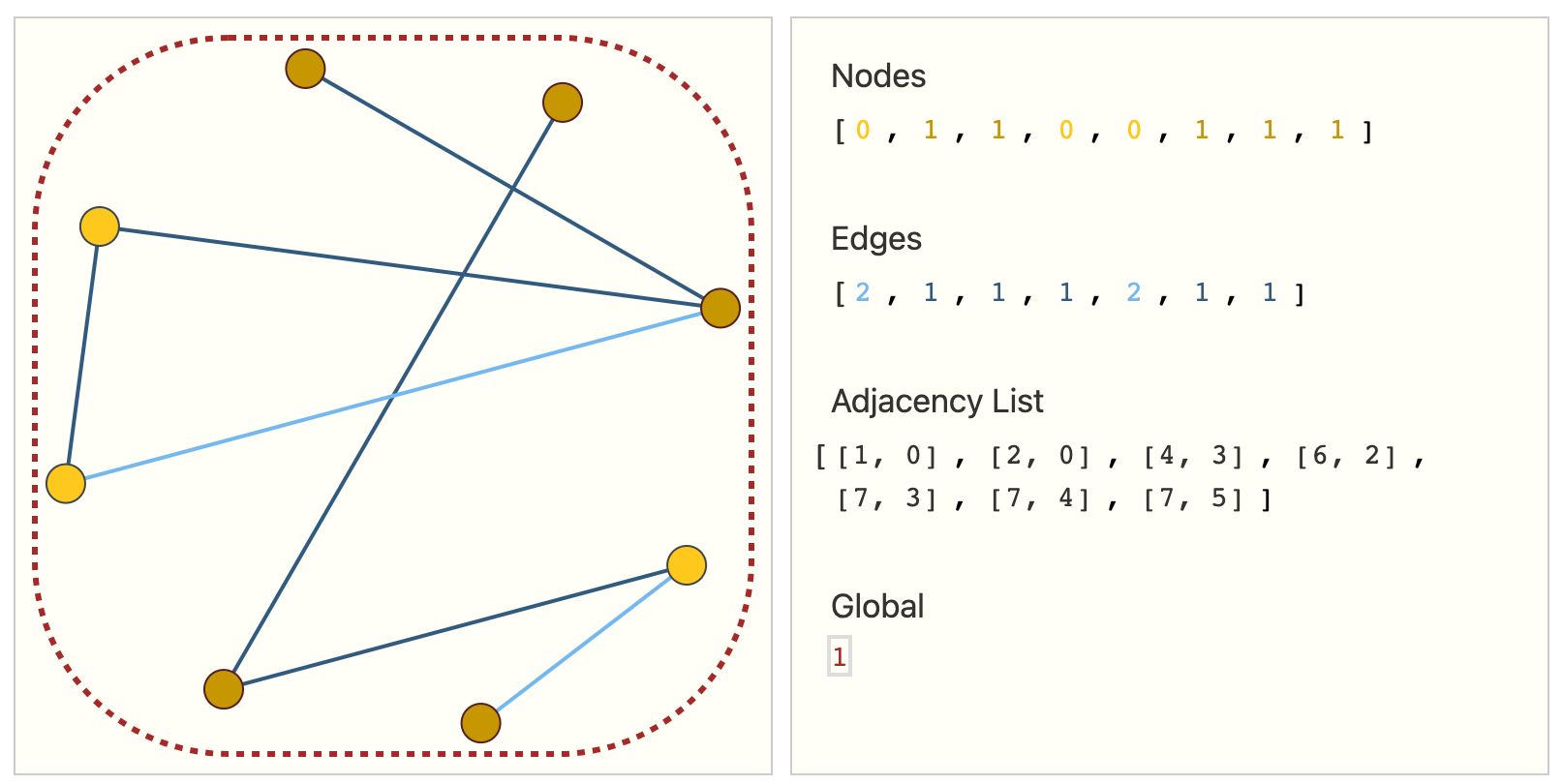
值得注意的是，该图中使用了每个节点/边/全局的标量值，但大多数实际的张量表示会有每个图属性的向量。我们将处理大小为 [𝑛_{𝑛𝑜𝑑𝑒𝑠},𝑛𝑜𝑑𝑒_{𝑑𝑖𝑚}] 的节点张量，而不是大小为 [𝑛_{𝑛𝑜𝑑𝑒𝑠}] 的节点张量。其他图属性也是如此。

图神经网络

现在图的描述以一个置换不变的矩阵格式呈现出来，我们将描述如何使用图神经网络（GNN）来解决图预测任务。GNN是对图的所有属性（节点、边、全局上下文）进行优化的变换，它保留了图的对称性（置换不变性）。我们将使用Gilmer等人提出的“消息传递神经网络”框架[18]，并借助Battaglia等人引入的Graph Nets架构示意[19]来构建GNN。GNN采用了“图输入，图输出”的架构，这意味着这些模型类型接受一个图作为输入，将信息加载到其节点、边和全局上下文中，并逐渐转换这些嵌入，而不改变输入图的连接性。

最简单的图神经网络

有了我们上面构建的图的数值表示（使用向量而不是标量），我们现在可以开始构建一个GNN。我们将从最简单的GNN架构开始，其中我们为所有图属性（节点、边、全局）学习新的嵌入，但我们还不使用图的连接性。

为了简单起见，前面的图示中使用标量来表示图的属性；实际上，特征向量或嵌入更加实用。你也可以称其为GNN块，因为它包含多个操作/层（类似于ResNet块）。

这个GNN在图的每个组件上使用一个单独的多层感知器（MLP）（或者你喜欢的可微分模型）；我们将其称为一个GNN层。对于每个节点向量，我们应用MLP并得到一个经过学习的节点向量。对于每条边，我们也是如此，学习每条边的嵌入，对于全局上下文向量也是如此，学习整个图的单一嵌入。

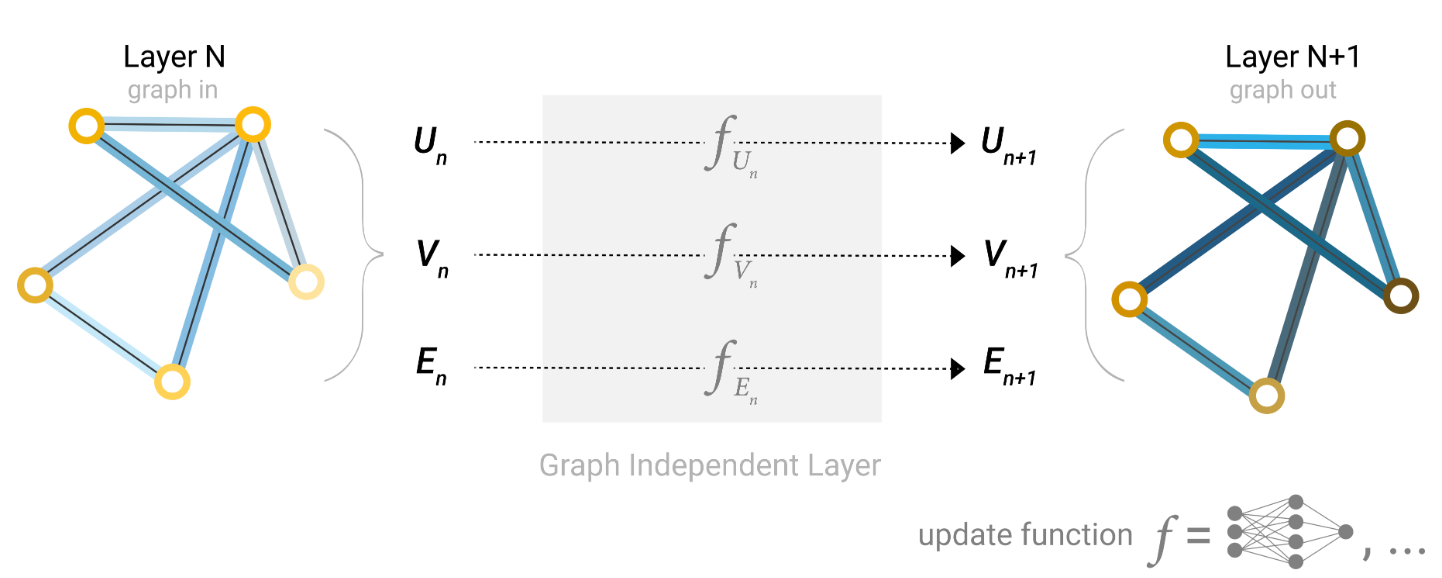
简单GNN的单个层。一个图形是输入，每个组件(V、E、U)都通过MLP进行更新以产生一个新的图形。每个函数的下标表示GNN模型的第n层中不同图属性的单独函数。

与神经网络模块或层一样，我们可以将这些GNN层堆叠在一起。

由于GNN不会更新输入图的连接性，我们可以用相同的邻接表和与输入图相同数量的特征向量来描述GNN的输出图。但是，输出图具有更新的嵌入，因为GNN已经更新了节点、边和全局上下文的表示。

通过汇集信息进行GNN预测

我们已经构建了一个简单的GNN，但是如何在我们上面描述的任何任务中进行预测呢？

我们将考虑二元分类的情况，但是这个框架可以很容易地扩展到多类别或回归的情况。如果任务是在节点上进行二元预测，并且图已经包含节点信息，那么方法很简单——对于每个节点嵌入，应用一个线性分类器。

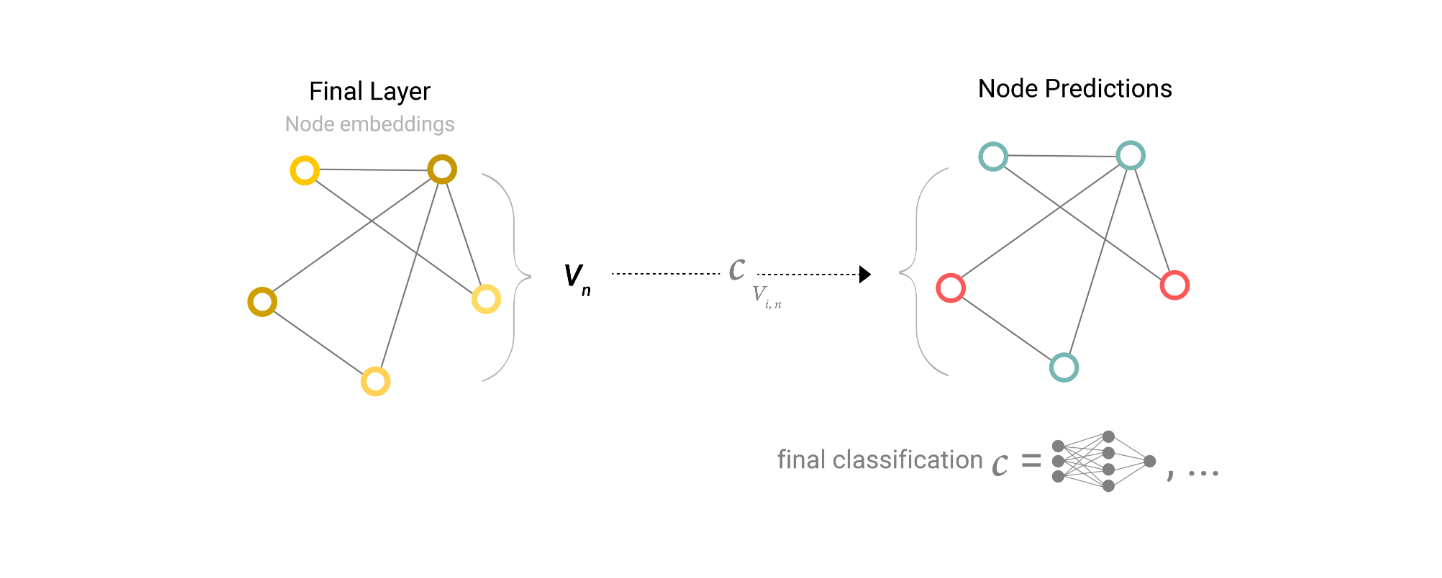
我们可以想象一个社交网络，我们希望通过不使用用户数据（节点），而只使用关系数据（边）来实现匿名化。这样的情况之一是我们在“节点级任务”小节中指定的节点任务。在空手道俱乐部的例子中，这只是使用人们之间的会议次数来确定对Mr. Hi或John H的忠诚度。

然而，并不总是这么简单的。例如，你可能在图中的边缘存储了信息，但在节点中没有信息，但仍然需要对节点进行预测。我们需要一种方法来从边缘收集信息并将其传递给节点进行预测。我们可以通过汇集来实现这一点。汇集分为两个步骤：

1. 对于每个要汇聚的项目，收集它们的每个嵌入并将它们连接成一个矩阵。

2. 然后通过一个汇总操作来对收集到的嵌入进行聚合，通常是求和操作。

   如果想更深入地讨论聚合操作，请转到“比较聚合操作”部分。

我们用符号 𝑝 来表示汇聚操作，并表示我们从边到节点的信息收集为 𝑝_{𝐸𝑛→𝑉𝑛}。

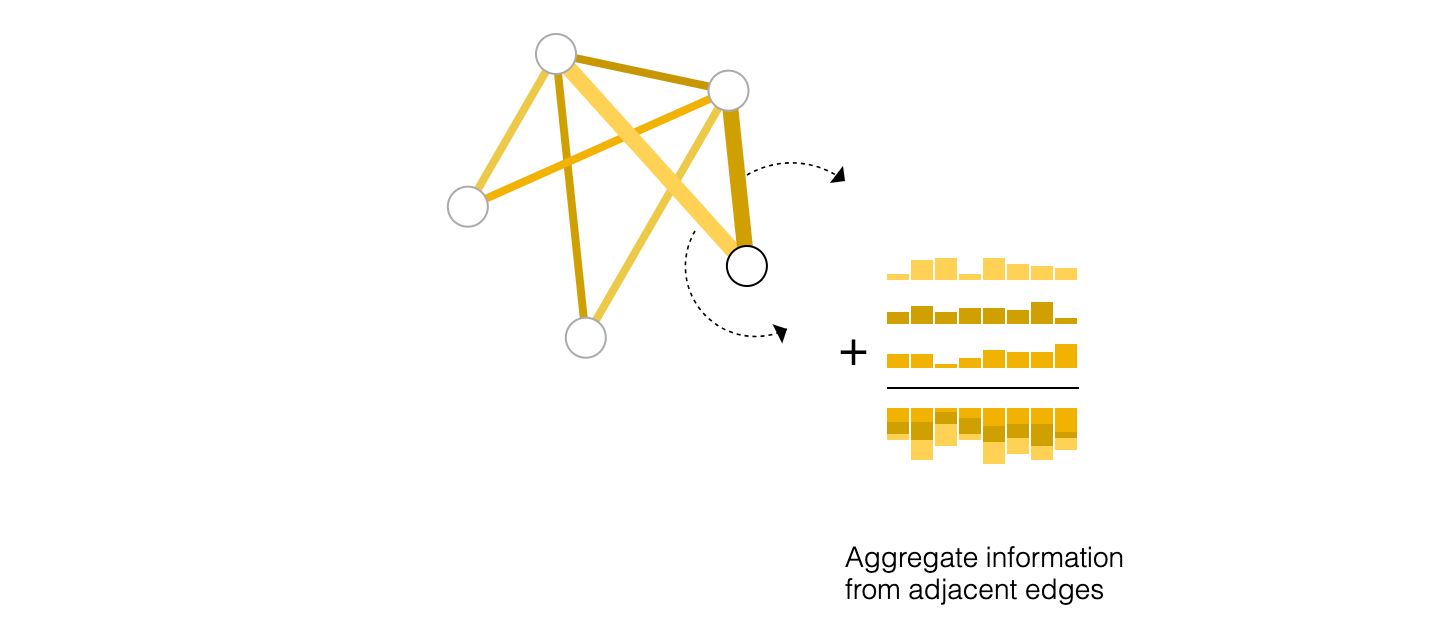
因此，如果我们只有边级特征，并试图预测二元节点信息，我们可以使用汇聚来将信息传递到需要的位置。模型看起来像这样。

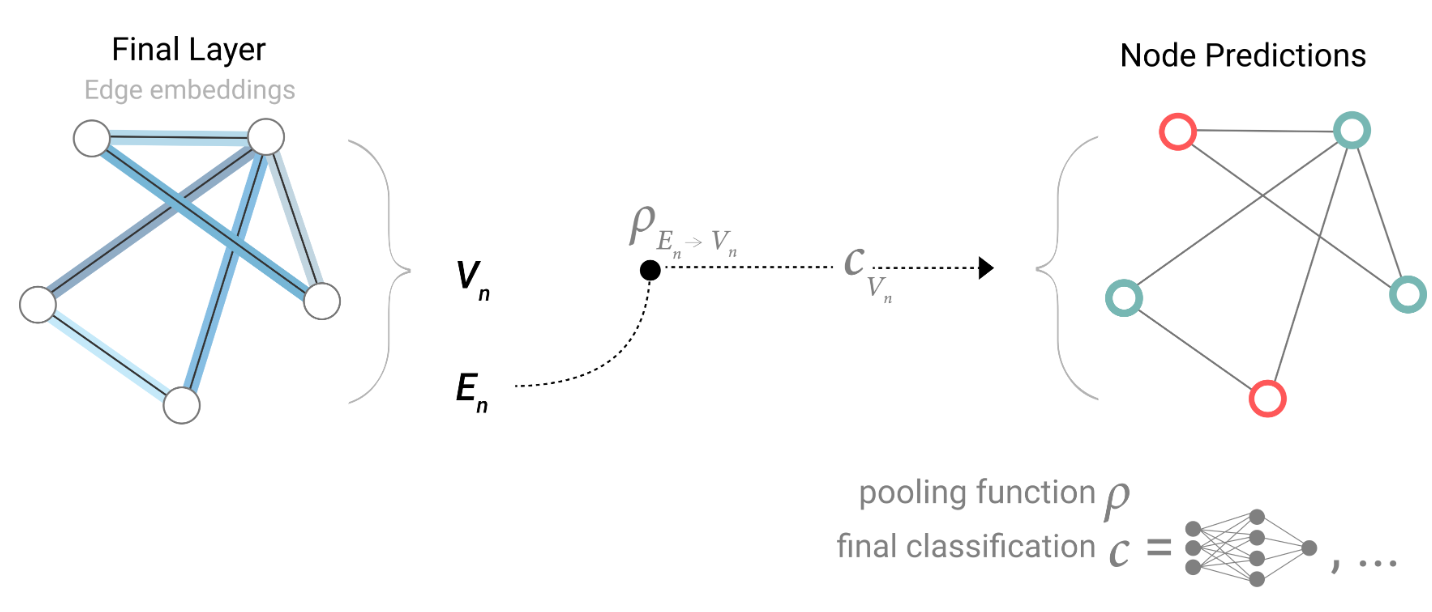
如果我们只有节点级特征，并试图预测二元边级信息，模型看起来像这样。

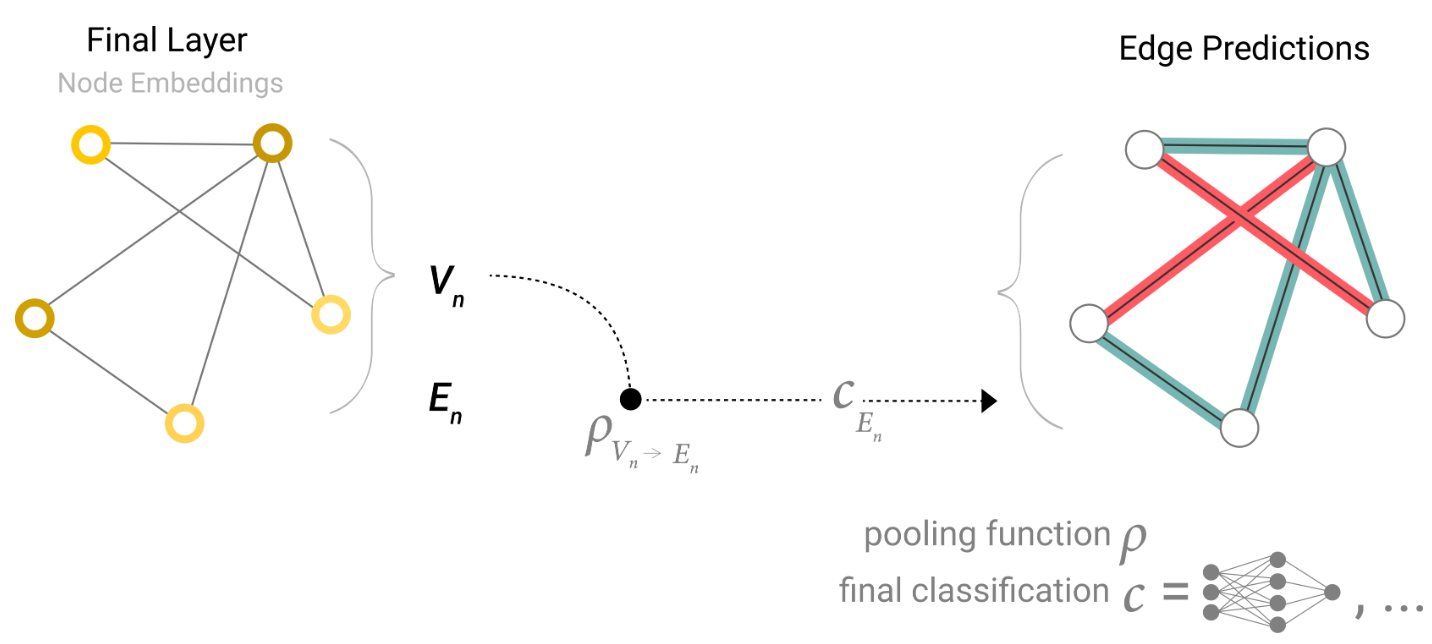
这样一个情景的一个例子是我们在边级任务小节中指定的边任务。节点可以被识别为图像实体，我们试图预测实体是否共享一个关系（二元边）。

如果我们只有节点级特征，需要预测一个二元的全局属性，我们需要将所有可用的节点信息收集在一起并进行聚合。这类似于卷积神经网络中的全局平均池化层。对于边也可以做同样的操作。

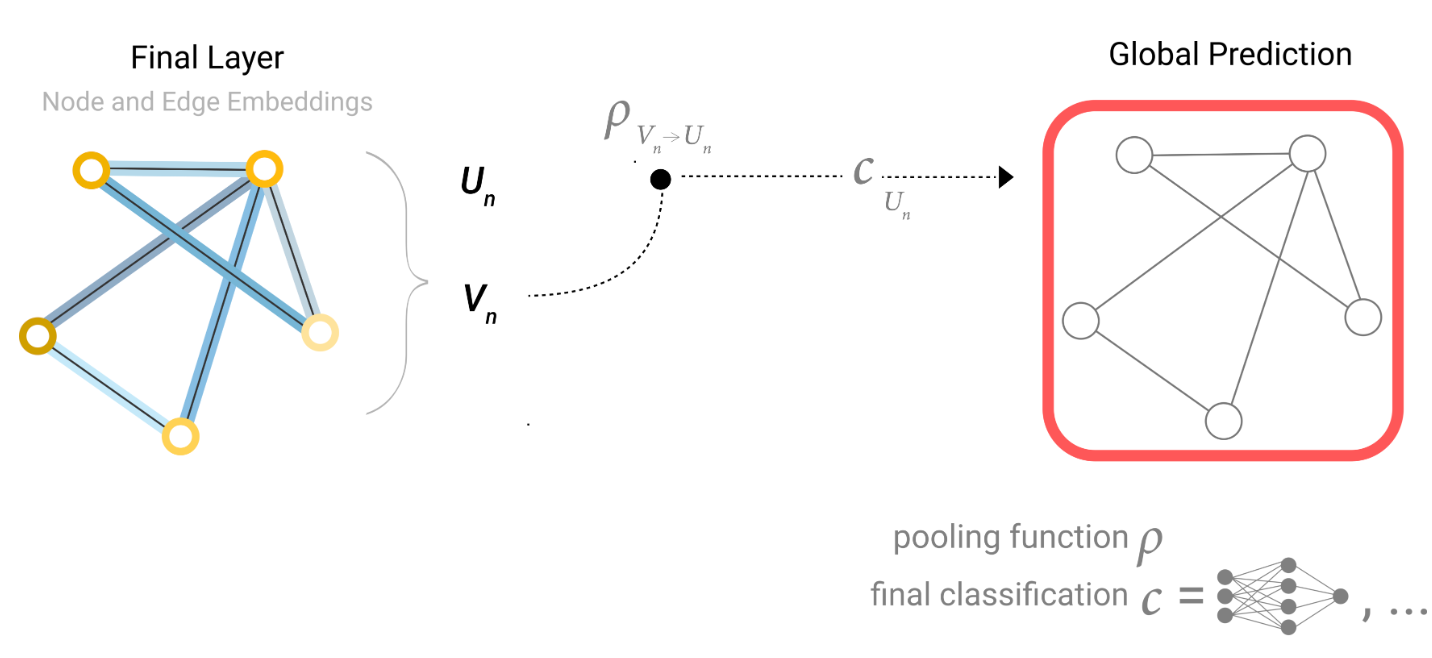
在我们的示例中，分类模型 𝑐 可以轻松地被任何可微分模型取代，或者可以通过使用广义线性模型来进行多类分类的适应。

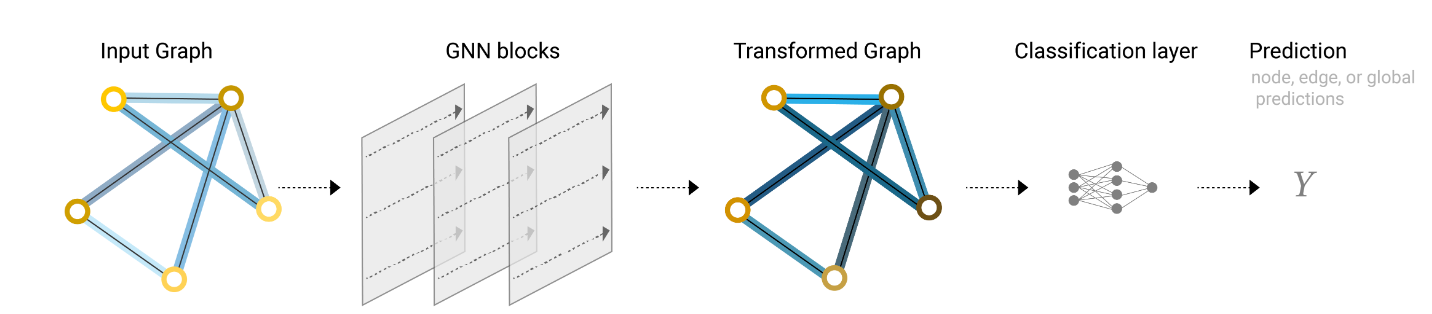
一个端到端的GNN预测

现在我们已经演示了如何构建一个简单的GNN模型，并通过在图的不同部分之间传递信息来进行二元预测。这种汇聚技术将作为构建更复杂的GNN模型的基石。如果我们有新的图属性，我们只需定义如何将信息从一个属性传递到另一个属性。

请注意，在这个最简单的GNN公式中，在GNN层内部我们根本不使用图的连接性。每个节点都是独立处理的，每条边也是如此，全局上下文也是如此。只有在汇聚信息进行预测时才使用连接性。

在图的各部分之间传递消息

我们可以通过在GNN层内部使用汇聚来进行更复杂的预测，以使我们学到的嵌入能够感知图的连接性。我们可以使用消息传递来实现这一点，即相邻节点或边交换信息并影响彼此更新后的嵌入。

消息传递分为三个步骤：

1. 对于图中的每个节点，收集所有相邻节点的嵌入（或消息），这是上面描述的 𝑔 函数。

2. 通过聚合函数（如求和）对所有消息进行聚合。

3. 所有汇聚的消息都通过一个更新函数传递，通常是一个学习的神经网络。

你也可以先收集消息，然后更新它们，最后聚合它们，仍然可以得到一个置换不变的操作。

就像汇聚可以应用于节点或边一样，消息传递可以发生在节点或边之间。

这些步骤对于利用图的连接性至关重要。我们将构建更复杂的消息传递变体，以产生表达力和能力不断增强的GNN模型。

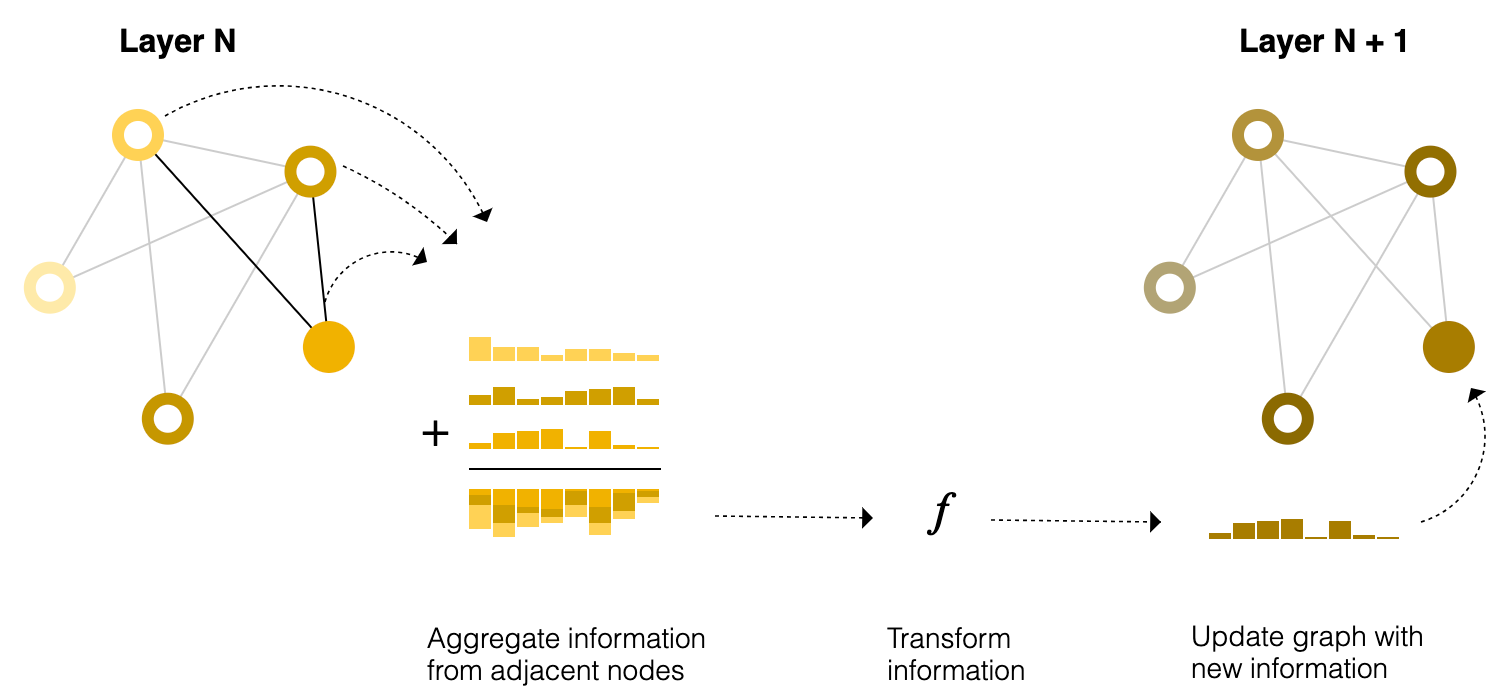
将鼠标悬停在一个节点上，以突出显示相邻节点，并可视化将进行汇总、更新和存储的相邻嵌入。

这一系列的操作，当应用一次时，就构成了最简单的消息传递GNN层。

这让人想起了标准的卷积操作：实质上，消息传递和卷积都是为了聚合和处理一个元素的相邻元素的信息，以更新该元素的值。在图中，该元素是一个节点，在图像中，该元素是一个像素。然而，与图像中每个像素都有一组固定数量的相邻元素不同，在图中，相邻节点的数量可以是可变的。

通过堆叠消息传递GNN层，一个节点最终可以整合来自整个图的信息：经过三层后，一个节点对距离它三步的节点具有信息。

我们可以更新我们的架构图，以包括节点的这个新信息来源：

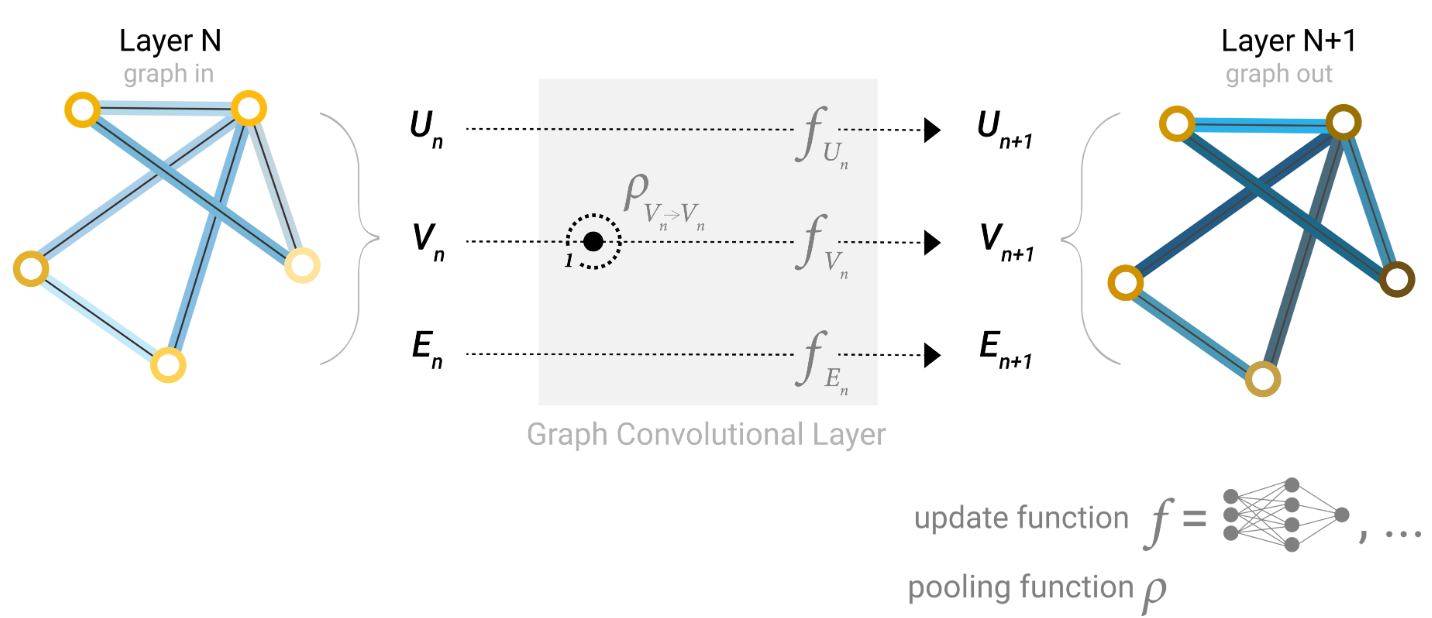
GCN架构的示意图，它通过在一个度的距离上聚合相邻节点来更新图的节点表示。

学习边的表示

我们的数据集并不总是包含所有类型的信息（节点、边和全局上下文）。当我们想要对节点进行预测，但我们的数据集只包含边信息时，我们在上面展示了如何在模型的最终预测步骤中使用汇聚将信息从边路由到节点。我们可以在GNN层内部使用消息传递在节点和边之间共享信息。

我们可以以与之前使用相邻节点信息相同的方式合并相邻边的信息，首先对边信息进行汇聚，然后用一个更新函数进行转换并存储它。

然而，在图中存储的节点和边的信息可能并不一定具有相同的大小或形状，因此如何将它们组合起来并不是立即明确的。一种方法是学习从边的空间到节点的空间的线性映射，反之亦然。另一种方法是在更新函数之前将它们连接在一起。

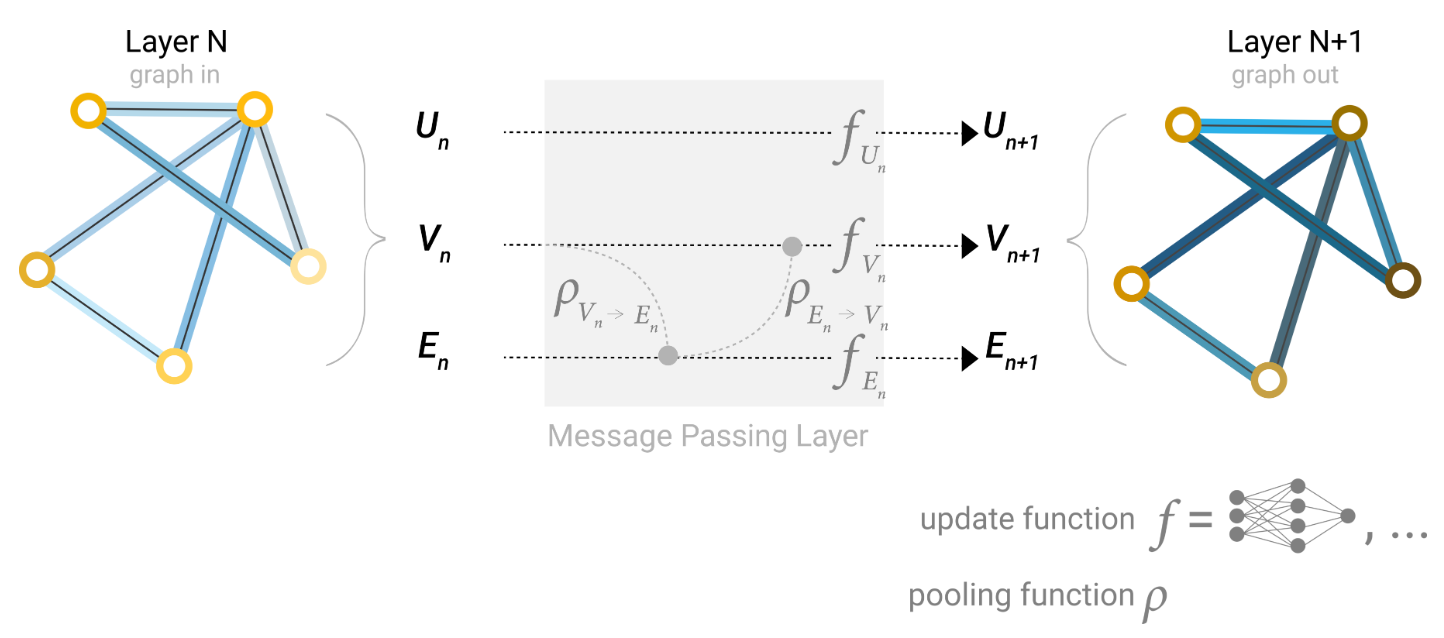
消息传递层的架构示意图。第一步“准备”了一个消息，其中包含了来自边及其连接的节点的信息，然后将消息“传递”给节点。

在构建GNN时，我们更新哪些图属性以及以何种顺序更新它们是一个设计决策。我们可以选择是在更新节点嵌入之前更新边嵌入，还是反过来。这是一个研究领域，有许多解决方案 – 例如，我们可以以“编织”方式进行更新，其中有四个更新的表示被合并成新的节点和边的表示：节点到节点（线性），边到边（线性），节点到边（边层），边到节点（节点层）。

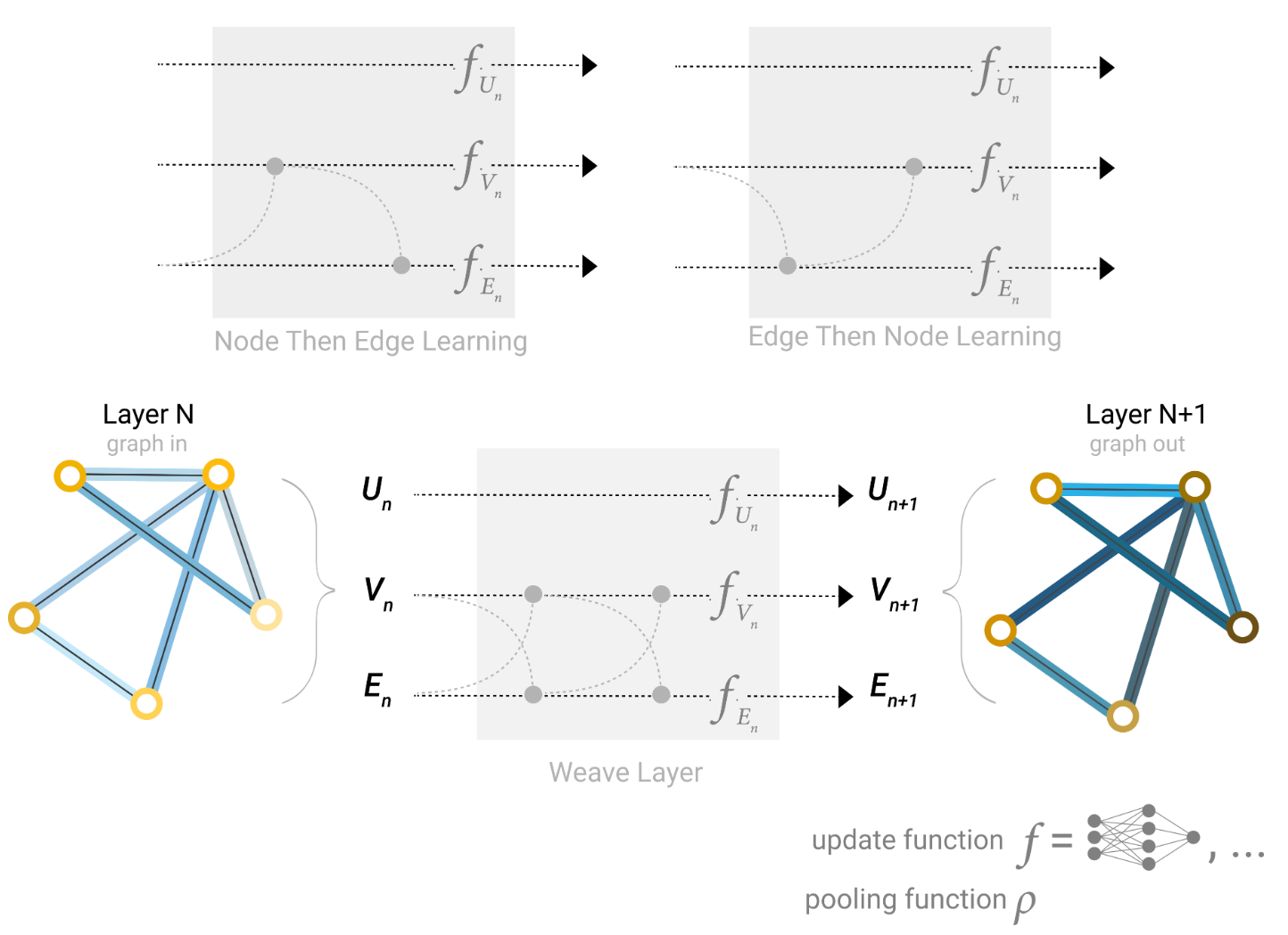
在GNN层中，我们可能结合边和节点表示的一些不同方式。

添加全局表示

到目前为止，我们描述的网络存在一个缺陷：在图中相距较远的节点可能永远无法有效地相互传递信息，即使我们多次应用消息传递也是如此。对于一个节点，如果我们有k层，信息最多会传播k步。这可能对依赖于相距较远的节点或节点组的预测任务造成问题。一个解决方案是使所有节点能够相互传递信息。然而，对于大型图形，这很快变得计算成本高昂（尽管对于小型分子等小图，已经使用了称为“虚拟边”的方法）。

解决此问题的一种方法是使用图的全局表示（U），有时称为主节点或上下文向量。这个全局上下文向量与网络中的所有其他节点和边相连接，并且可以作为它们之间传递信息的桥梁，从而构建了对整个图的表示。这比以其他方式学到的图的表示更丰富、更复杂。

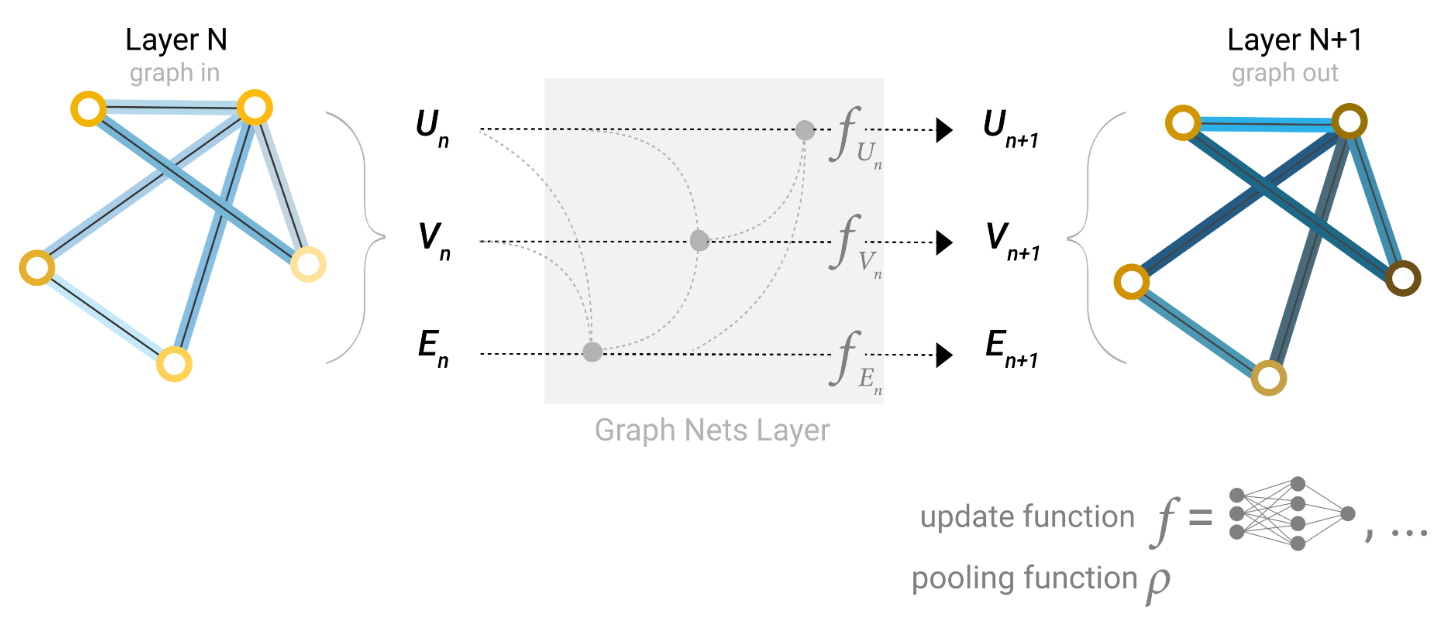
利用全局表示的图形网络架构示意图。

在这种视图中，所有的图属性都有了学习到的表示，因此我们可以在汇聚过程中利用它们，通过将我们感兴趣的属性的信息与其余属性相对应。例如，对于一个节点，我们可以考虑来自相邻节点、连接的边和全局信息的信息。为了将新的节点嵌入与所有这些可能的信息源相对应，我们可以简单地将它们连接起来。此外，我们还可以通过线性映射将它们映射到相同的空间并相加，或者应用一个特征调制层，这可以被看作是一种特征-wise 的注意机制。

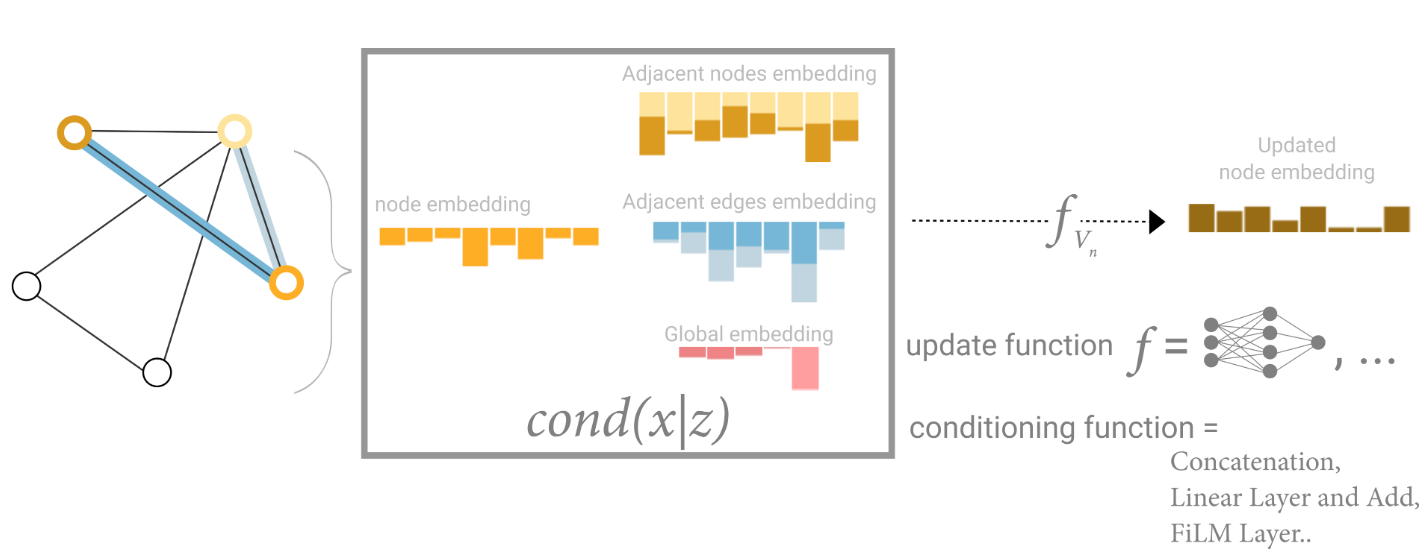
基于三个其他嵌入（相邻节点、相邻边、全局）来调整一个节点信息的示意图。这一步对应于图形网络层中的节点操作。

GNN游乐场

我们在这里描述了各种不同的GNN组件，但在实践中它们究竟有何区别呢？这个GNN游乐场允许你看到这些不同组件和架构如何影响GNN学习一个真实任务的能力。

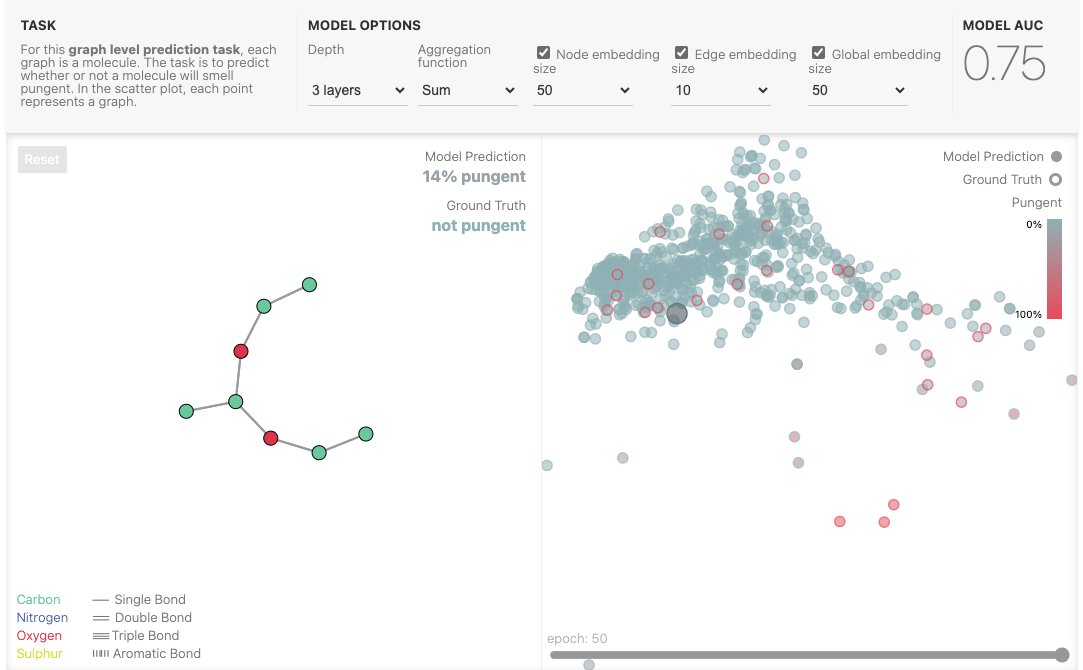
我们的游乐场展示了一个小分子图的图级别预测任务。我们使用了Leffingwell Odor数据集，该数据集由带有相关气味感知（标签）的分子组成。预测分子结构（图）与其气味之间的关系是一个涵盖了化学、物理、神经科学和机器学习的百年难题。

为了简化问题，我们只考虑每个分子的一个二元标签，即对分子图进行分类，判断其气味是否“辛辣”，由专业调香师标记。我们说一个分子具有“辛辣”的气味，如果它具有强烈、突出的气味。例如，大蒜和芥末可能含有烯丙醇分子，具有这种特性。而常用于薄荷味糖果的薄荷酮分子，也被描述为具有辛辣气味。

我们将每个分子表示为一个图，其中原子是节点，包含其原子种类的独热编码（碳、氮、氧、氟），化学键是边，包含其键类型的独热编码（单键、双键、三键或芳香键）。

我们解决这个问题的通用建模模板将通过逐层堆叠的GNN层构建，然后使用具有sigmoid激活函数的线性模型进行分类。我们的GNN模型的设计空间包括许多可以定制模型的杠杆：

1. GNN层的数量，也称为深度。
2. 更新时每个属性的维度。更新函数是一个具有relu激活函数和用于激活归一化的层规范的单层MLP。
3. 用于汇聚的聚合函数：最大、均值或求和。
4. 被更新的图属性，或消息传递的样式：节点、边和全局表示。我们通过布尔开关（开启或关闭）来控制这些选项。一个基线模型将是一个图独立的GNN（所有消息传递关闭），它在最后将所有数据汇聚到一个单一的全局属性中。打开所有消息传递功能将产生一个GraphNets架构。

为了更好地理解GNN如何学习一个任务优化的图形表示，我们还会查看GNN的倒数第二层激活。这些“图嵌入”是在预测之前GNN模型的输出。由于我们在预测中使用了广义线性模型，因此线性映射足以让我们看到如何围绕决策边界学习表示。

由于这些是高维向量，我们通过主成分分析（PCA）将它们降维到2D。一个完美的模型会清晰地将标记的数据分开，但由于我们在降维同时也有不完美的模型，这个边界可能会变得难以识别。

尝试使用不同的模型架构来建立你的直觉。例如，看看你是否可以编辑左侧的分子以增加模型的预测。相同的编辑对不同的模型架构是否产生相同的效果？

一些经验性的GNN设计教训

在上述探索架构选择时，您可能会发现某些模型的性能优于其他模型。是否有一些明确的GNN设计选择可以提供更好的性能？例如，深层GNN模型是否比较浅层的模型表现更好？或者在聚合功能之间是否有明确的选择？答案将取决于数据、[25] [26]，甚至不同的特征化和构建图的方法可能会得到不同的答案。

通过以下交互式图，我们将探讨GNN架构的空间以及在几个主要设计选择方面的任务性能：消息传递的方式、嵌入的维度、层数以及聚合操作类型。

散点图中的每个点代表一个模型：x轴是可训练变量的数量，y轴是性能。将鼠标悬停在一个点上，可以看到GNN架构参数。

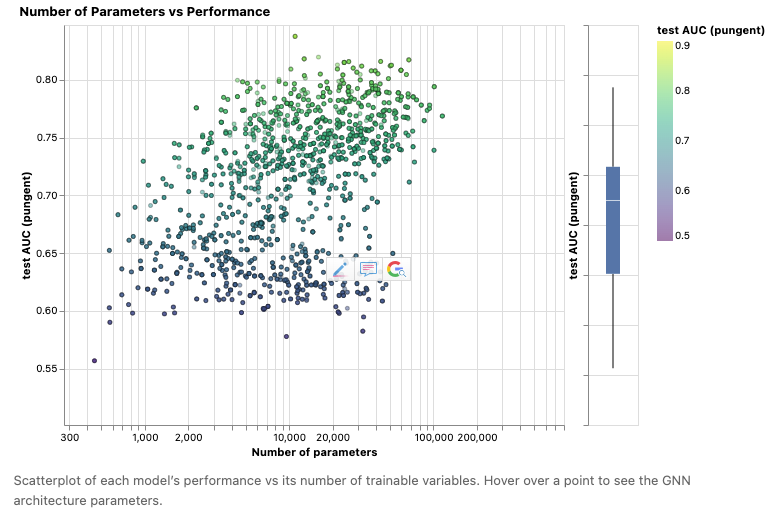
以上是每个模型性能与其可训练变量数量的散点图。将鼠标悬停在一个点上，可以看到 GNN 架构参数。

首先值得注意的是，令人惊讶的是，参数数量较高与性能较高呈正相关关系。 GNN 是一种非常高效的参数模型类型：即使对于很小的参数数量（3k），我们已经可以找到性能很高的模型。

接下来，我们可以查看根据不同图属性的学习表示的维度来汇总性能分布。

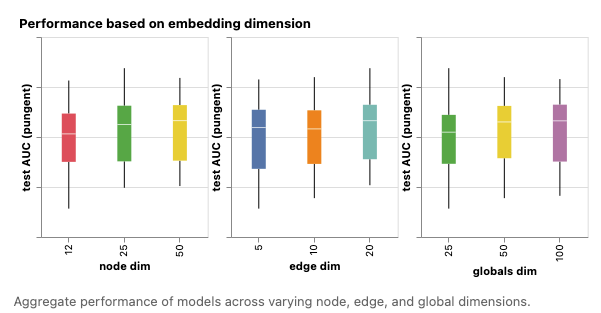
在不同节点、边和全局维度下，模型的总体性能。

我们可以注意到，具有更高维度的模型往往具有更好的平均性能和较低的下限性能，但最大性能并未出现相同的趋势。一些性能排名靠前的模型可以在较小的维度下找到。由于较高的维度也会涉及较高数量的参数，因此这些观察结果与前图相一致。

接下来，我们可以看到基于 GNN 层数的性能分布情况。

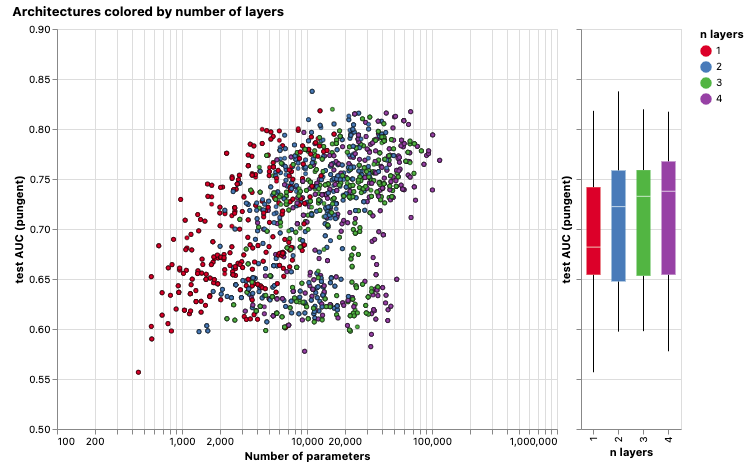
在图表中，显示了层数与模型性能之间的关系，以及模型性能与参数数量之间的关系。每个点的颜色代表了层数。将鼠标悬停在一个点上以查看GNN架构参数。

箱线图显示了类似的趋势，随着层数的增加，平均性能往往会提高，但表现最好的模型并不具有三层或四层，而是两层。此外，性能的下界随着四层而降低。这种效应之前已经被观察到过，具有更多层次的GNN将在更远的距离上广播信息，并且可能会冒着节点表示在许多连续迭代中被“稀释”的风险。

我们的数据集是否有首选的聚合操作？下图将性能按聚合类型进行了分解。

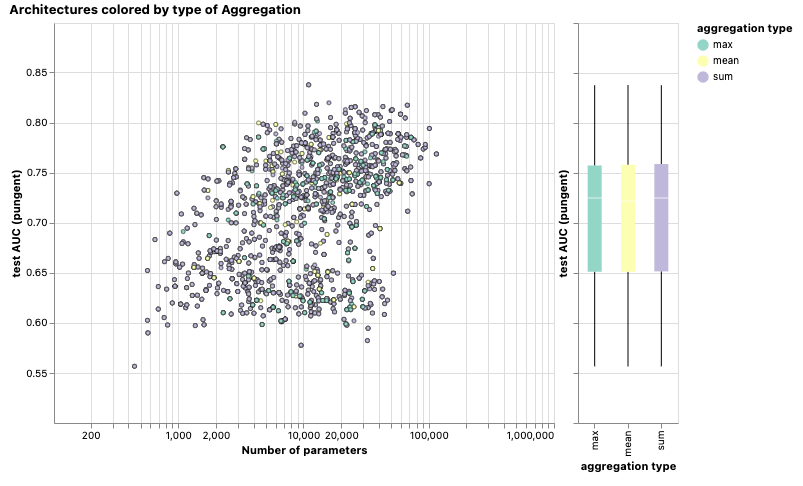
在这幅图中，我们可以看到在这个任务中，max池化似乎稍微优于其他两种池化方式。然而，这也取决于具体的数据集和任务，不同的情况下可能会有不同的结果。另外，我们还可以看一下关于消息传递的不同风格对模型性能的影响。

在这个图表中，我们可以看到在这个任务中，没有消息传递的模型（“none”）性能相对较差，而同时传递信息给节点、边和全局属性的模型在平均性能上更为优越。

总的来说，通过这些探索，我们可以看到了一些模型设计的一般趋势，但也发现了一些相反的例子。这再次强调了模型设计的复杂性，不同的因素可能会在不同的情况下产生不同的影响。

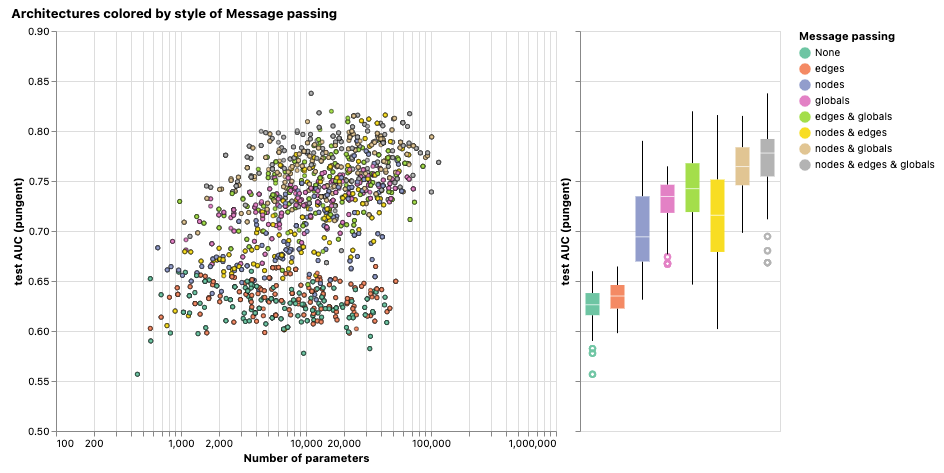
这张图表展示了基于消息传递风格的性能对比，同时也包括了模型性能与可训练参数数量的散点图。每个点的颜色表示了消息传递的方式。将鼠标悬停在点上可以查看GNN架构的参数。

总体而言，我们可以看到，与图属性间的交流越多，平均模型的性能越好。我们的任务集中在全局表示上，因此明确地学习这个属性也往往会提高性能。我们还发现节点表示比边表示更有用，这也很合理，因为节点属性中加载了更多信息。

从这里可以朝着两个一般方向去追求更好的性能。一个与更复杂的图算法相关，另一个与图本身相关。

到目前为止，我们的GNN基于一个基于邻域的汇聚操作。有一些图的概念在这种方式下更难以表达，例如线性图路径（由节点构成的连通链）。设计一种新的机制，可以在GNN中提取、执行和传播图信息，是当前的研究方向之一。

GNN研究的前沿之一不是创建新的模型和架构，而是“如何构建图”，更确切地说，是赋予图附加的结构或关系，以便利用。正如我们所看到的，与图属性间的交流越多，我们往往会有更好的模型。在这种情况下，我们可以考虑使分子图更加丰富，方法是在节点之间添加额外的空间关系，添加非键的边，或在子图之间添加显式可学习的关系。

进一步深入

接下来，我们有一些关于与GNN相关的各种图形相关主题的章节。

其他类型的图（多重图，超图，超节点，分层图）

虽然我们只描述了每个属性具有矢量化信息的图，但图结构更加灵活，可以容纳其他类型的信息。幸运的是，消息传递框架足够灵活，通常将GNNs适应更复杂的图结构是通过定义如何传递和更新新的图属性来实现的。

例如，我们可以考虑多边图或多重图，其中一对节点可以共享多种类型的边，当我们希望基于其类型来建模节点之间的交互时，就会发生这种情况。例如，在社交网络中，我们可以根据关系类型（熟人，朋友，家人）指定边缘类型。可以通过为每种边缘类型设置不同类型的消息传递步骤来调整GNN。我们还可以考虑嵌套图，例如一个节点代表一个图，也称为超节点图。嵌套图对于表示分层信息非常有用。例如，我们可以考虑一个分子网络，其中一个节点表示一个分子，如果我们有一种方法（反应）将一个分子转化为另一个分子，那么它们之间就共享一个边。在这种情况下，我们可以通过训练期间在分子级别和反应网络级别之间学习表示的GNN来在嵌套图上学习。

另一种类型的图是超图，其中一个边可以连接到多个节点，而不仅仅是两个。对于给定的图，我们可以通过识别节点的社区并分配与社区中所有节点连接的超边来构建超图。

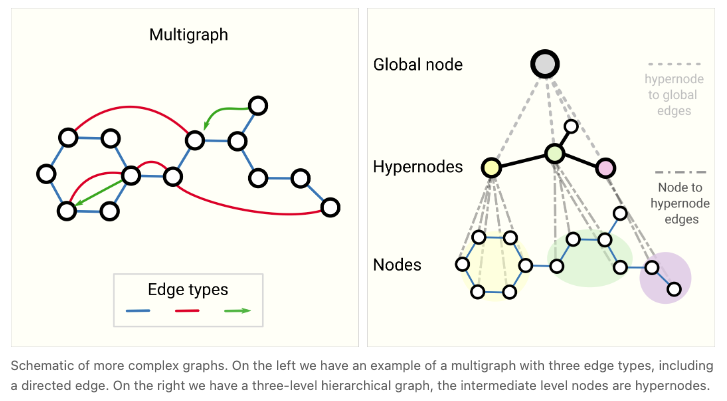
更复杂图形的示意图。左侧是一个具有三种边类型的多重图示例，包括一个有向边。右侧是一个三层次的分层图，中间层节点是超节点。

如何训练和设计具有多种图属性的GNN是当前的研究方向。

在GNNs中抽样图形和批处理

训练神经网络的一种常见方法是使用在训练数据的随机常量大小子集（小批量）上计算的梯度来更新网络参数。由于图中节点和边的数量相邻的节点和边之间的变化很大，因此这种做法对于图形构成了挑战，无法使用常量批量大小。关于图形批处理的主要思想是创建保留较大图形的基本属性的子图。这种图形抽样操作高度依赖于上下文，并涉及从图形中选择节点和边。这些操作在某些情况下可能是有意义的（引用网络），而在其他情况下，这些操作可能会过于强大（分子，其中一个子图仅表示一个新的、较小的分子）。如何对图进行抽样是一个尚未解决的研究问题。如果我们关心保留邻域级别的结构，一种方法是随机抽样一个均匀数量的节点，构成节点集合。然后添加距离k的邻接节点，包括它们的边。每个邻域可以视为一个单独的图，并且可以在这些子图的批次上对GNN进行训练。损失可以被遮蔽，只考虑节点集合，因为所有相邻节点都具有不完整的邻域。更高效的策略可能是首先随机抽样一个单一节点，扩展其邻域到距离k，然后从扩展集中选择另一个节点。这些操作可以在构建一定数量的节点、边或子图后终止。如果上下文允许，我们可以通过选择初始节点集，然后通过随机、随机游走或Metropolis算法等方式对一定数量的节点进行子抽样来构建具有恒定大小邻域的子图。

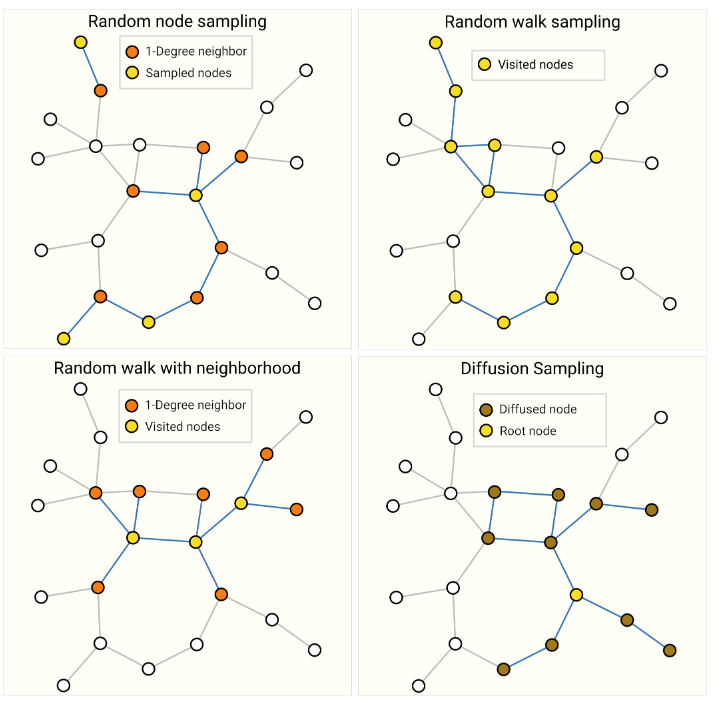
这里展示了对同一图进行抽样的四种不同方式。抽样策略的选择高度依赖于上下文，因为它们会生成不同的图统计数据分布（节点数量、边数量等）。对于高度连接的图，也可以对边进行子抽样。

对于无法完全加载到内存的大型图，进行图抽样尤其重要。这种情况已经启发了新的架构和训练策略，比如Cluster-GCN和GraphSaint。我们预计未来图数据集的规模将继续增长。

归纳偏差

在构建用于解决特定类型数据问题的模型时，我们希望专门针对该数据的特性进行模型定制。成功实现这一点时，通常会看到更好的预测性能、更短的训练时间、更少的参数以及更好的泛化性能。

举个例子，当在图像上标记时，我们希望利用这样一个事实，即无论一只狗出现在图像的左上角还是右下角，它仍然是一只狗。因此，大多数图像模型使用卷积，它们具有平移不变性。对于文本来说，标记的顺序非常重要，因此循环神经网络会按顺序处理数据。此外，一个标记的存在（例如单词“not”）可以影响句子其余部分的含义，因此我们需要组件能够“关注”文本的其他部分，而像BERT和GPT-3这样的变换器模型可以做到这一点。这些都是归纳偏差的一些例子，我们在数据中识别对称性或规律，并添加利用这些特性的建模组件。

在处理图时，我们关心每个图组件（边、节点、全局）之间的关系，因此我们寻求具有关系归纳偏差的模型。模型应该保留实体之间的显式关系（邻接矩阵），并保留图的对称性（置换不变性）。我们期望那些实体之间的交互很重要的问题将从图结构中受益。具体来说，这意味着设计对集合的转换：对节点或边的操作顺序不应该重要，而且操作应该适用于可变数量的输入。

比较聚合操作

从相邻节点和边中汇总信息是任何合理强大的GNN架构中的关键步骤。由于每个节点具有可变数量的邻居，并且因为我们希望使用一个可微分的方法来聚合这些信息，我们希望使用一种平滑的聚合操作，它对节点顺序和提供的节点数量不变。

选择和设计最优聚合操作是一个开放的研究课题。聚合操作的一个理想属性是相似的输入会产生相似的聚合输出，反之亦然。一些非常简单的候选排列不变操作包括求和、均值和最大值。类似方差的总结统计信息也可以工作。所有这些操作都接受可变数量的输入，并提供相同的输出，无论输入的顺序如何。让我们探讨一下这些操作之间的区别。

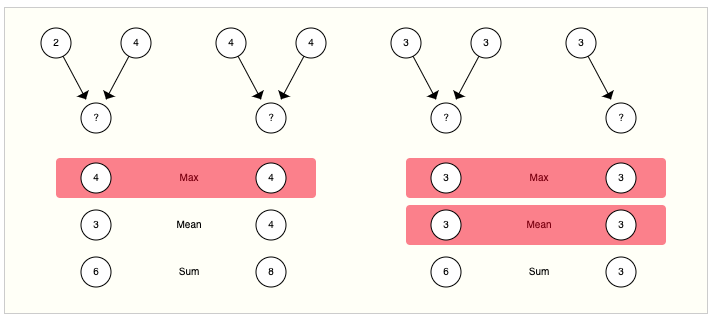
没有一种汇聚类型总是能够区分左侧的最大值汇聚和右侧的求和/均值汇聚等图对。

没有一种操作在所有情况下都是最佳选择。均值操作在节点邻居数量变化很大或者需要对本地邻域的特征进行归一化视图时可能很有用。最大操作在您想要突出显示本地邻域中单一显著特征时可能很有用。求和在这两者之间提供了平衡，它提供了本地特征分布的快照，但由于它没有进行归一化，也可能突出显示离群值。在实践中，通常使用求和。

设计聚合操作是一个开放的研究问题，它与集合上的机器学习交叉。新方法，比如主要邻域聚合，通过将它们串联起来并添加一个依赖于待聚合实体的连接度的缩放函数，同时考虑了几种聚合操作。同时，也可以设计特定于领域的聚合操作。一个例子是“四面体手性”聚合运算符。

将GCN视为子图函数逼近器

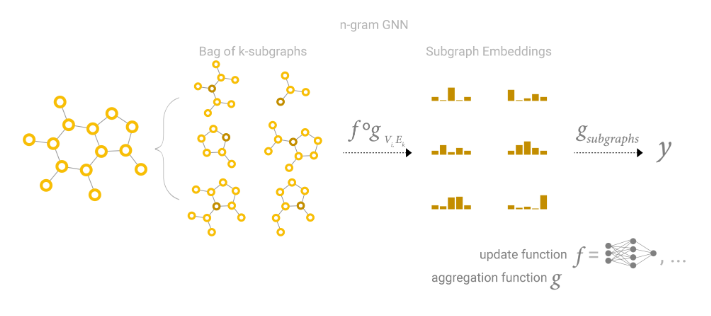
GCN（以及MPNN）在具有1度邻居查找的情况下，可以看作是一个操作在大小为k的子图上的学习嵌入的神经网络。

当关注一个节点时，在k层之后，更新后的节点表示对所有距离为k的邻居具有有限的视角，本质上是子图表示。对于边表示也是如此。

因此，GCN正在收集所有可能的大小为k的子图，并从一个节点或边的角度学习向量表示。可能的子图数量可以组合地增长，因此从一开始枚举这些子图与在GCN中动态构建它们可能会不切实际。

边和图的对偶关系

一个需要注意的事情是，尽管边的预测和节点的预测看似不同，但通常可以归结为相同的问题：在图𝐺上的边预测任务可以表述为在𝐺的对偶上进行的节点级别预测。

要获得𝐺的对偶，我们可以将节点转换为边（将边转换为节点）。一个图及其对偶包含相同的信息，只是以不同的方式表达出来。有时，这种性质使得在一个表示中解决问题比在另一个表示中更容易，就像在傅里叶空间中的频率一样。简而言之，要在𝐺上解决边分类问题，我们可以考虑在𝐺的对偶上进行图卷积（这与在𝐺上学习边表示是相同的），这个想法是由Dual-Primal图卷积网络发展而来的。

图卷积作为矩阵乘法，以及矩阵乘法作为图上的遍历

我们已经讨论了许多关于图卷积和消息传递的内容，当然，这引发了一个实际上如何实现这些操作的问题。在本节中，我们将探讨矩阵乘法、消息传递以及它们与图遍历的联系的一些特性。

我们首先要说明的一点是，邻接矩阵 𝐴 （大小为 𝑛_{𝑛𝑜𝑑𝑒𝑠}×𝑛_{𝑛𝑜𝑑𝑒𝑠} ）与节点特征矩阵 𝑋（大小为 𝑛_{𝑛𝑜𝑑𝑒𝑠}×𝑛𝑜𝑑𝑒𝑠_{dim} ）的矩阵乘法实现了一种简单的消息传递，其中包括了求和聚合。设矩阵为 𝐵=𝐴𝑋 ，我们可以观察到任何条目 𝐵_{𝑖𝑗} 都可以表示为 <𝐴_{𝑟𝑜𝑤_𝑖}𝑋_{𝑐𝑜𝑙𝑢𝑚𝑛_𝑗}>=𝐴_{𝑖,1}𝑋_{1,𝑗}+𝐴_{𝑖,2}𝑋_{2,𝑗}+…+𝐴_{𝑖,𝑛}𝑋_{𝑛,𝑗}=\sum_{𝐴_{𝑖,𝑘}>0}𝑋_{𝑘,𝑗} 。因为 𝐴_{𝑖,𝑘} 只有在节点 𝑛𝑜𝑑𝑒_𝑖 与节点 𝑛𝑜𝑑𝑒_𝑘 之间存在边的情况下才为二进制条目，所以内积实际上是在“收集”所有与节点 𝑛𝑜𝑑𝑒_𝑖 共享边的维度为 𝑗的节点特征值。值得注意的是，这种消息传递并不会更新节点特征的表示，只是汇聚相邻节点的特征。但是通过在矩阵相乘之前或之后将𝑋 通过您喜爱的可微变换（例如 MLP）传递，可以轻松地进行适应。

从这个视角来看，我们可以欣赏到使用邻接表的好处。由于 𝐴 的预期稀疏性，我们不必对所有 𝐴_{𝑖,𝑗} 为零的值进行求和。只要我们有一种基于索引来收集值的操作，我们就可以只检索正条目。此外，这种无需矩阵乘法的方法使我们摆脱了将求和作为聚合操作的必要性。

我们可以想象多次应用这个操作可以让我们在更大的距离上传播信息。从这个意义上说，矩阵乘法是一种在图上遍历的形式。当我们观察邻接矩阵的幂 𝐴^𝐾时，这种关系也是显而易见的。如果我们考虑矩阵 𝐴^2，那么 𝐴^2_{𝑖𝑗} 就统计了从节点 𝑛𝑜𝑑𝑒_𝑖 到 𝑛𝑜𝑑𝑒_𝑗 的长度为2的所有路径，并且可以表示为内积 <𝐴_{𝑟𝑜𝑤_𝑖}𝑋_{𝑐𝑜𝑙𝑢𝑚𝑛_𝑗}>=𝐴_{𝑖,1}𝑋_{1,𝑗}+𝐴_{𝑖,2}𝑋_{2,𝑗}+…+𝐴_{𝑖,𝑛}𝑋_{𝑛,𝑗}=\sum_{𝐴_{𝑖,𝑘}>0}𝑋_{𝑘,𝑗}。直观上，第一个 𝑎_{𝑖,1}𝑎_{1,𝑗} 仅在两种情况下为正值：存在连接 𝑛𝑜𝑑𝑒_𝑖 与 𝑛𝑜𝑑𝑒_1 的边，以及存在连接 𝑛𝑜𝑑𝑒_𝑖 与 𝑛𝑜𝑑𝑒_j 的边。换句话说，这两条边形成了一条长度为2的路径，从 𝑛𝑜𝑑𝑒_𝑖 到𝑛𝑜𝑑𝑒_j经过了 𝑛𝑜𝑑𝑒_1 。由于求和，我们对所有可能的中间节点进行计数。当考虑 𝐴^3=𝐴𝐴^2.. 等等直至 𝐴𝑘 时，这一直观也会保持。

图注意网络

另一种在图属性之间传递信息的方法是通过注意力机制。例如，当我们考虑节点及其1度相邻节点的汇总时，我们也可以考虑使用加权和。此时的挑战在于以一种排列不变的方式关联权重。一种方法是考虑一个标量评分函数，它基于节点对 𝑓(𝑛𝑜𝑑𝑒_𝑖,𝑛𝑜𝑑𝑒_𝑗)分配权重。在这种情况下，评分函数可以解释为衡量相邻节点与中心节点的关联性的函数。权重可以被归一化，例如通过 softmax 函数，以便将大部分权重集中在与任务相关的相邻节点上。这个概念是图注意力网络（Graph Attention Networks，GAT） [53] 和集合变换器（Set Transformers）[54]的基础。由于评分是在节点对上进行的，排列不变性得以保持。常见的评分函数是内积（inner product），并且通常在评分之前，节点会通过线性映射转化为查询和键向量，以增加评分机制的表达能力。此外，为了可解释性，评分权重可以用作衡量边对任务的重要性的指标。

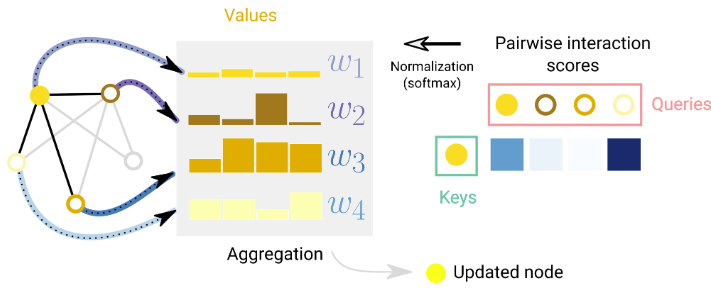
对于一个节点，相对于其相邻节点的注意力示意图。对于每条边，计算一个交互得分，对其进行归一化，并用于加权节点嵌入。

此外，可以将变压器视为带有注意力机制的GNN。从这个角度来看，变压器将多个元素（例如字符标记）建模为一个全连接图中的节点，并且注意力机制将为每对节点分配边嵌入，这些边嵌入用于计算注意力权重。两者的区别在于它们对实体之间连接模式的假设，GNN 假定稀疏连接模式，而变压器则模拟了所有连接。

图解释和归因

在实际应用中，我们可能关心模型的可解释性，以建立可信度、调试或进行科学发现。我们关心的图概念因上下文而异。例如，在分子领域，我们可能关心特定子图的存在或缺失，而在引文网络中，我们可能关心文章的连接程度。由于图概念的多样性，有许多方法可以构建解释。GNNExplainer 将这个问题视为提取对任务重要的最相关的子图。归因技术为图的部分分配了排名的重要性值，这些部分与任务相关。由于可以合成具有现实性和挑战性的图问题，因此 GNN 可以作为一个严格且可重复的测试平台，用于评估归因技术。

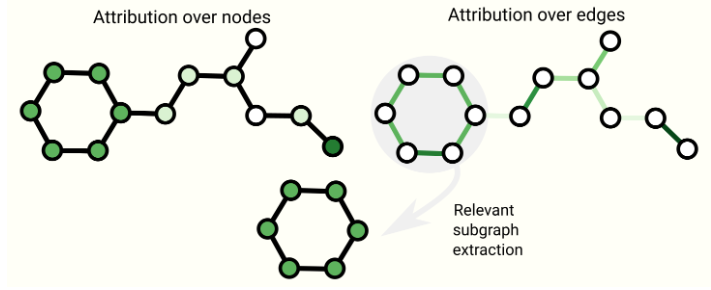
图中展示了一些图解释技术的示意图。归因技术为图属性分配了排名的值。这些排名可以用作提取与任务相关的连接子图的基础。

生成模型

除了在图上学习预测模型外，我们可能还关心在图上学习生成模型。通过生成模型，我们可以从学习到的分布中进行采样或在给定一个起始点的情况下生成新的图。一个相关的应用是在设计新药物时，需要具有特定属性的新分子图作为治疗疾病的候选者。

图生成模型的一个关键挑战在于建模图的拓扑结构，它的大小可能会发生显著变化，并且具有 𝑁^2_{𝑛𝑜𝑑𝑒𝑠} 项。一个解决方案是直接像处理图像一样来对待邻接矩阵，采用自动编码器框架。[60]将存在或不存在边的预测视为二元分类任务。可以通过仅预测已知的边以及不存在的部分边来避免 𝑁^2_{𝑛𝑜𝑑𝑒𝑠} 项。图形变分自动编码器 (graphVAE) 学会了对邻接矩阵中的连接性和部分非连接性模式进行建模。

另一种方法是通过从一个图开始，然后迭代地应用诸如添加或删除节点和边等离散动作来逐步构建图。为了避免为离散动作估计梯度，我们可以使用策略梯度。这可以通过自回归模型（如 RNN）[61] 来实现，或者在强化学习场景中[62] 进行。此外，有时可以将图形建模为具有语法元素的序列[63][64]。

最后的思考

图形是一种强大且丰富的结构化数据类型，其优势和挑战与图像和文本完全不同。在本文中，我们概述了研究人员在构建处理图形的基于神经网络的模型方面取得的一些里程碑。我们讨论了在使用这些架构时必须做出的一些重要设计选择，希望 GNN 平台可以让你对这些设计选择的实证结果有直观的认识。近年来 GNN 在许多领域取得的成功为解决一系列新问题提供了绝佳的机会，我们期待着看到该领域会带来什么样的成果。