矩阵分解技术用于推荐系统

Yehuda Koren, Yahoo Research Robert Bell and Chris Volinsky, AT&T Labs—Research

正如Netflix Prize竞赛所证明的那样，矩阵分解模型在生成产品推荐方面优于传统的最近邻技术，可以整合额外的信息，如隐式反馈、时间效应和置信度水平。

整合额外的信息，如隐式反馈、时间效应和置信水平

现代消费者面临着无尽的选择。电子零售商和内容提供商提供了大量的产品选择，为满足各种特殊需求和口味提供了前所未有的机会。将消费者与最合适的产品匹配是提高用户满意度和忠诚度的关键。因此，越来越多的零售商对推荐系统产生了兴趣，这些系统通过分析用户对产品的兴趣模式，提供适合用户口味的个性化推荐。由于良好的个性化推荐可以为用户体验增添另一个维度，亚马逊和Netflix等电子商务领军企业已将推荐系统作为其网站的重要组成部分。

这样的系统对于电影、音乐和电视节目等娱乐产品特别有用。许多用户会观看同一部电影，而每个用户可能会观看许多不同的电影。用户已经证明愿意表达对特定电影的满意程度，因此有大量关于哪些电影吸引哪些用户的数据可供使用。公司可以分析这些数据，向特定的用户推荐电影。

强调了推荐系统在娱乐产品领域的重要性和适用性。它们可以帮助电子零售商和内容提供商更好地匹配用户与适合他们口味的产品，从而提高用户的满意度和忠诚度。特别是对于电影、音乐和电视节目等娱乐产品，由于用户对这些产品的满意度能够得到明确的反馈，所以有大量的数据可用于分析，以了解哪些产品适合哪些用户，并根据这些数据为用户推荐合适的产品。

推荐系统的策略

广义上，推荐系统基于两种策略之一。内容过滤策略通过为每个用户或产品创建个人资料来描述其特征。例如，电影个人资料可以包括关于其类型、参演演员、票房口碑等方面的属性。用户个人资料可能包括人口统计信息或在适当问卷中提供的答案。这些个人资料使程序能够将用户与相匹配的产品关联起来。当然，内容过滤策略需要收集可能不易获取或难以收集的外部信息。

内容过滤的一种成功实现是音乐基因项目（Music Genome Project），该项目被用于互联网广播服务Pandora.com。训练有素的音乐分析师根据数百个不同的音乐特征对Music Genome Project中的每首歌曲进行评分。这些属性或基因不仅捕捉了歌曲的音乐特性，还包括许多与理解听众音乐偏好相关的重要品质。

与内容过滤相反的另一种方法仅依赖于过去的用户行为，例如以往的交易记录或产品评价，而无需创建明确的用户配置文件。这种方法被称为协同过滤，这个术语是由第一个推荐系统Tapestry的开发者创造的。协同过滤分析用户之间的关系和产品之间的相互依赖关系，以识别新的用户-项目关联。

给出了协同过滤的定义 Collaborative filtering：协同过滤

协同过滤的一个重要优点是它不受领域限制，但它可以处理内容过滤往往难以捉摸和难以建立配置文件的数据方面。虽然通常比基于内容的技术更准确，但协同过滤存在所谓的冷启动问题，即无法处理系统的新产品和用户。在这方面，内容过滤更具优势。

协同过滤的两个主要领域是邻域方法和潜在因子模型。邻域方法侧重于计算物品之间或用户之间的关系。以物品为导向的方法通过同一用户对“相邻”物品的评分来评估用户对某个物品的偏好。一个产品的相邻物品是那些当同一用户对它们进行评分时得到类似评分的其他产品。例如，考虑电影《拯救大兵瑞恩》。它的相邻物品可能包括战争电影、史蒂文·斯皮尔伯格的电影和汤姆·汉克斯的电影等。要预测特定用户对《拯救大兵瑞恩》的评分，我们将寻找该用户实际评分过的该电影的最近邻物品。如图1所示，以用户为导向的方法可以识别志同道合的用户，他们可以相互补充评分。

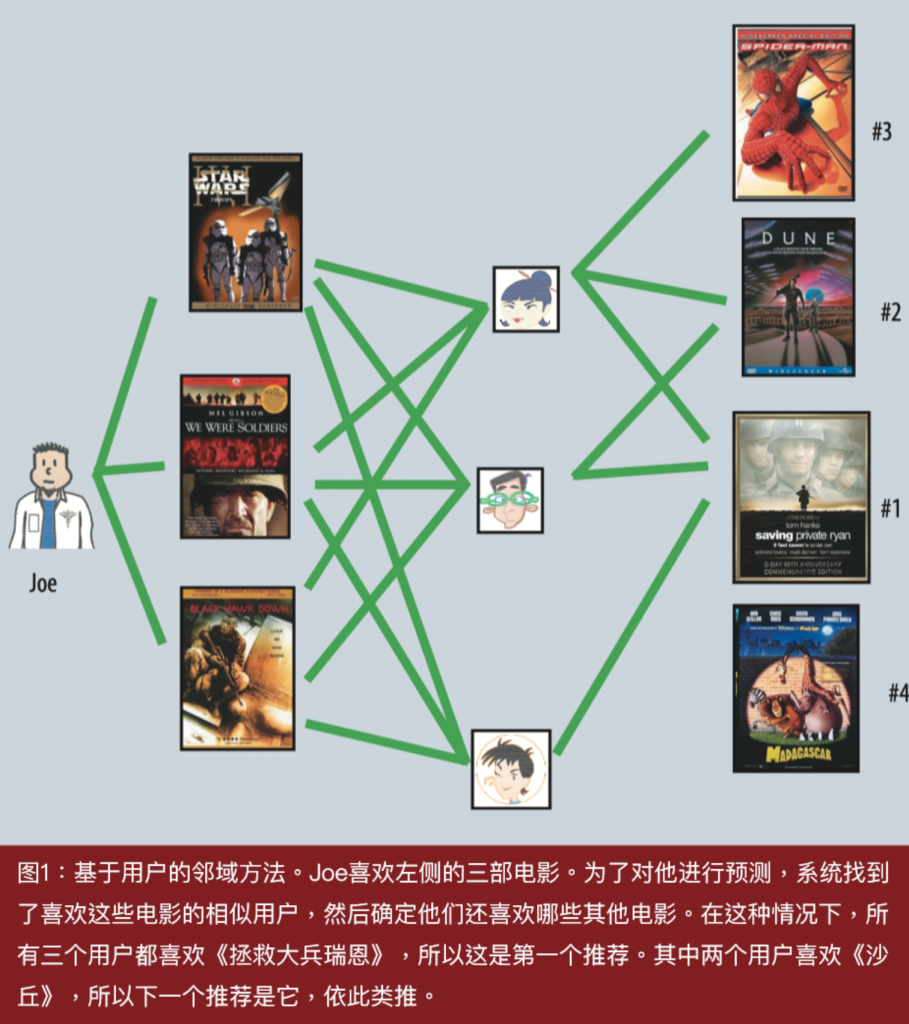
潜在因子模型是一种替代方法，它试图通过从评分模式中推断的20到100个因子来描述物品和用户，以解释评分。从某种意义上说，这些因子构成了人工创造的歌曲基因的计算机化替代品。对于电影，发现的因子可能衡量明显的维度，如喜剧与戏剧、动作的数量或面向儿童的倾向；不太明确的维度，如角色发展的深度或怪癖；或者完全无法解释的维度。对于用户来说，每个因子衡量的是用户对在相应电影因子上得分高的电影的喜好程度。

图2 以两个维度的简化示例阐述了这个想法。考虑两个假设的维度，分别为女性导向与男性导向以及严肃与逃避现实。图中显示了一些知名电影和一些虚构用户可能在这两个维度上的位置。对于这个模型，用户对电影的预测评分与电影在图上的位置和用户在图上的位置的点积相等，相对于电影的平均评分。例如，我们预计Gus会喜欢《呆子与呆贼》，讨厌《紫色》，并将《勇敢的心》评为平均水平。注意，一些电影（例如《欧洲攻略》）和用户（例如Dave）在这两个维度上被认为是相对中性的。

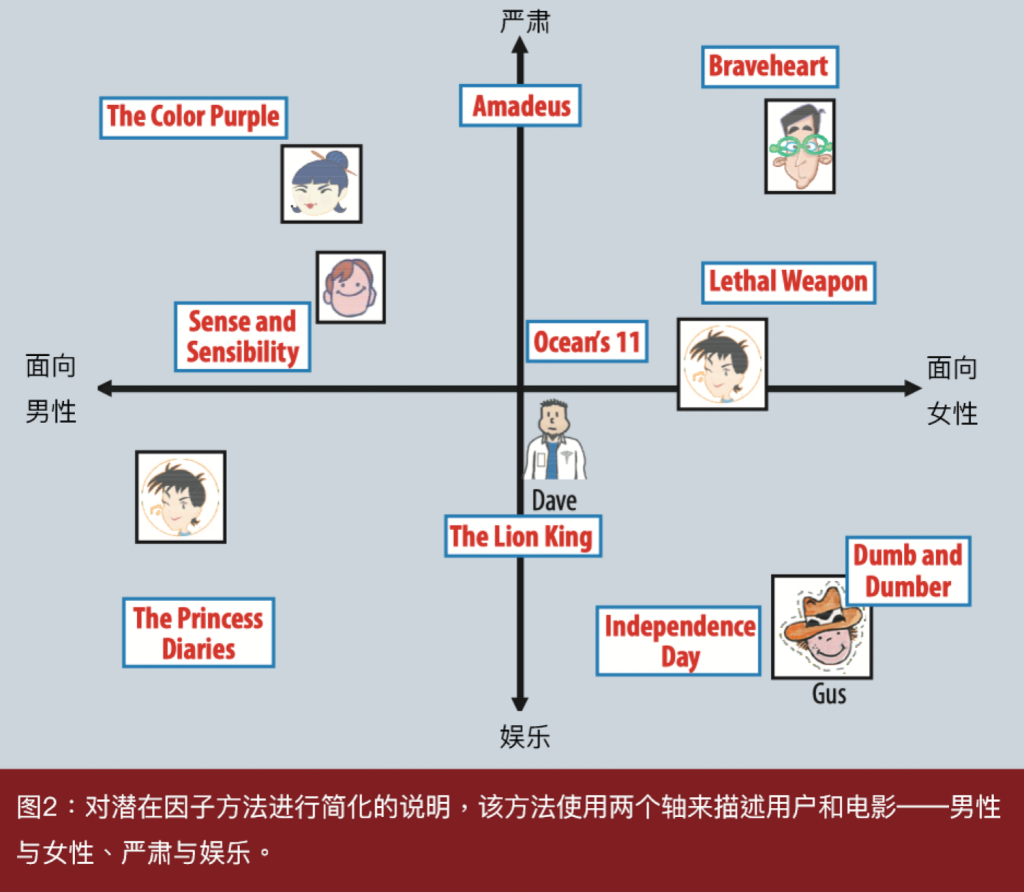
讨论了推荐系统的策略，主要涉及两种策略：内容过滤和协同过滤。内容过滤策略通过创建用户和产品的个人资料来描述它们的特征。协同过滤是依赖于用户的过去行为。尽管协同过滤可以处理内容过滤难以捉摸的数据方面，但它存在冷启动问题，即无法处理系统的新产品和用户。

矩阵分解方法

一些最成功的潜在因子模型的实现基于矩阵分解。在其基本形式中，矩阵分解通过从物品评分模式中推断的因子向量来描述物品和用户。物品因子和用户因子之间的高相似度可以用于进行推荐。这些方法近年来变得流行起来，因为它们在可扩展性和预测准确性方面表现良好。此外，它们还提供了在建模各种实际情况时的很大灵活性。

推荐系统依赖不同类型的输入数据，通常将这些数据放置在一个矩阵中，其中一维表示用户，另一维表示感兴趣的物品。最方便的数据是高质量的显式反馈，包括用户对产品兴趣的明确输入。例如，Netflix收集电影的星级评价，TiVo用户通过按赞和踩按钮来表示他们对电视节目的偏好。我们将明确的用户反馈称为评分。通常情况下，明确的反馈构成了一个稀疏矩阵，因为任何单个用户只可能对一小部分可能的物品进行评分。

矩阵分解的一个优点是它允许加入额外的信息。当没有显式反馈可用时，推荐系统可以使用隐式反馈来推断用户的偏好，隐式反馈通过观察用户行为间接反映意见，包括购买历史、浏览历史、搜索模式甚至鼠标移动。隐式反馈通常表示事件的存在或不存在，因此通常由一个填充密集的矩阵表示。

该内容讨论了潜在因子模型的一种实现方式——矩阵分解，并介绍了矩阵分解在推荐系统中的应用。

基本的矩阵分解模型

矩阵分解模型将用户和物品映射到一个维度为f的共同潜在因子空间，使得用户-物品交互可以在该空间中建模为内积。因此，每个物品i都与一个向量q_i ∈ R^f相关联，每个用户u都与一个向量p_u ∈ R^f相关联。对于给定的物品i，q_i的元素度量了物品在这些因子上的积极或消极程度。对于给定的用户u，p_u的元素度量了用户对具有相应因子的高分物品的兴趣程度，同样可以是积极或消极的。得到的点积q_i^Tp_u捕捉了用户u和物品i之间的交互——用户对物品特征的整体兴趣。这近似于用户u对物品i的评分，用r_{ui}表示，从而得出估计值。

\hat{r}_{ui}=q_i^Tp_u

主要的挑战是计算每个物品和用户到因子向量q_i,p_u ∈ R^f的映射。在推荐系统完成这个映射之后，可以通过使用方程式1轻松地估计用户对任何物品的评分。

这样的模型与奇异值分解（Singular Value Decomposition，SVD）密切相关，SVD是信息检索中用于识别潜在语义因子的一种成熟技术。在协同过滤领域应用SVD需要对用户-物品评分矩阵进行因子分解。由于用户-物品评分矩阵的稀疏性导致大量缺失值，这常常带来困难。当矩阵的知识不完整时，传统的SVD是未定义的。此外，仅仅对相对较少的已知条目进行处理很容易导致过拟合问题。

早期的系统依靠填充缺失评分来使评分矩阵变得密集。然而，填充操作可能非常昂贵，因为它显著增加了数据量。此外，不准确的填充可能会严重扭曲数据。因此，近期的研究建议直接对观测到的评分进行建模，同时通过正则化模型避免过拟合。为了学习因子向量（p_u和q_i），系统在已知评分集上最小化正则化的平方误差：

min\sum_{(u,i)\in  κ}(r_{ui}-q^T_ip_u)^2+\lambda(||q_i||^2+||p_u||^2)

这里，κ是已知r_{ui}的(u, i)对的集合（训练集）。

该系统通过拟合先前观测到的评分来学习模型。然而，目标是以一种能够预测未来未知评分的方式来推广这些先前的评分。因此，系统应该通过对学到的参数进行正则化来避免对观测数据过拟合，其大小受到惩罚。常数λ控制正则化的程度，通常通过交叉验证确定。Ruslan Salakhutdinov和Andriy Mnih的《概率矩阵分解》提供了正则化的概率基础。

学习算法

最小化方程2的两种方法是随机梯度下降（stochastic gradient descent）和交替最小二乘法（alternating least squares，ALS）。

随机梯度下降

Simon Funk在(http://sifter.org/~simon/journal/20061211.html)
中推广了对方程2的随机梯度下降优化算法，其中该算法遍历训练集中的所有评分。对于每个给定的训练样本，系统预测r_{ui}并计算相关的预测误差。

e_{ui}=r_{ui}-q^T_ip_u

然后，它按照梯度相反方向与g成正比的大小修改参数，得到：

·\ \ q_i\leftarrow q_i+\gamma ·(e_{ui}·p_u-\lambda q_i)\\
·\ \ p_u\leftarrow p_u+\gamma ·(e_{ui}·q_i-\lambda p_u)

这种流行的方法（4-6）结合了易于实现和相对较快的运行时间。然而，在某些情况下，使用交替最小二乘法（ALS）优化是有益的。

交替最小二乘法

因为q_i和p_u 都是未知数，所以方程2不是凸的。然而，如果我们固定其中一个未知数，优化问题就变成了二次型，并可以被最优解求解。因此，交替最小二乘法（ALS）的技术在固定q_i 和固定p_u 之间进行交替。当所有的p_u 被固定时，系统通过求解一个最小二乘问题重新计算q_i ，反之亦然。这确保每一步都会减小方程2直到收敛。

虽然通常情况下，随机梯度下降比ALS更简单且更快，但是在至少两种情况下，ALS更有优势。第一种情况是系统可以使用并行化。在ALS中，系统独立计算每个q_i ，而与其他物品因子无关，同时独立计算每个p_u ，而与其他用户因子无关。这为算法提供了潜在的大规模并行计算的可能性。第二种情况是对于以隐式数据为中心的系统。由于训练集不能被认为是稀疏的，对每个单独的训练样本进行循环——就像梯度下降那样——是不实际的。ALS可以有效地处理这种情况。

加入偏差

矩阵分解方法在协同过滤中的一个好处是其灵活性，可以处理各种数据方面和其他特定应用的要求。这要求在保持相同的学习框架的同时对方程1进行调整。方程1试图捕捉用户和物品之间产生不同评分值的交互作用。然而，观察到的评分值的很大一部分变化是由与用户或物品相关的效应引起的，这些效应被称为偏差或截距，与任何交互作用无关。例如，典型的协同过滤数据表现出某些用户给出的评分比其他用户更高，某些物品收到的评分比其他物品更高的系统性倾向。毕竟，某些产品被普遍认为比其他产品更好（或更差）。

因此，仅通过q_i^T p_u的交互来解释完整的评分值是不明智的。相反，系统试图确定个别用户或物品偏差可以解释的这些值的部分，并将数据中仅有真正的交互部分进行因子建模。评分r_{ui} 中涉及的偏差的一阶近似如下所示：

b_{ui}=\mu+b_i+b_u

评分r_{ui}中涉及的偏差被表示为b_{ui}，它考虑了用户和物品的影响。整体平均评分用\mu表示；参数b_u和b_i分别表示用户u和物品i相对于平均值的观测偏差。例如，假设您想要对用户Joe对电影《泰坦尼克号》的评分进行一阶估计。现在假设所有电影的平均评分\mu为3.7星级。此外，泰坦尼克号优于平均水平，所以它的评分往往比平均值高出0.5星。另一方面，Joe是一个挑剔的用户，他的评分往往比平均值低0.3星。因此，Joe对《泰坦尼克号》的评分估计将是3.9星（3.7 + 0.5 – 0.3）。偏差将方程1扩展如下：

\hat{r}_{ui}=\mu+b_i+b_u+q^T_ip_u

在这里，观测到的评分被分解为四个组成部分：全局平均、物品偏差、用户偏差和用户物品交互。这样每个组成部分只解释与其相关的部分信号。系统通过最小化平方误差函数来进行学习：

\min_{p*,q*,b*}
\sum_{(u,i)\in  κ}(r_{ui}-\mu-b_u-b_i-q^T_ip_u)^2+\lambda(||q_i||^2+||p_u||^2+b_u^2+b_i^2)

由于偏差往往捕捉到观测信号的很大部分，因此准确建模它们是至关重要的。因此，其他研究提供了更复杂的偏差模型。

额外的输入来源

通常，系统必须处理冷启动问题，即许多用户提供非常少的评分，导致很难对他们的喜好做出一般性结论。缓解这个问题的方法是结合关于用户的额外信息来源。推荐系统可以使用隐式反馈来了解用户的偏好。事实上，它们可以收集行为信息，而不受用户提供明确评分的意愿的限制。例如，零售商可以利用客户的购买记录或浏览历史来了解他们的倾向，除了这些客户可能提供的评分外。

为了简化起见，考虑一种具有布尔隐式反馈的情况。N(u)表示用户u表达了隐式偏好的物品集合。通过用户隐式偏好的物品，系统对用户进行个人画像。在这里，需要一个新的物品因子集合，其中物品i与x_i ∈ R^f相关联。因此，对于在N(u)中显示了对物品偏好的用户，其特征向量为：

\sum_{i\in N(u)}x_i

通常对和进行归一化是有益的，例如，使用以下方式进行处理：

|N(u)|^{-0.5}\sum_{i\in N(u)}x_i

另一个信息来源是已知的用户属性，例如人口统计信息。同样，为了简化起见，考虑布尔属性，其中用户u对应于属性集合A(u)，该集合可以描述性别、年龄组、邮政编码、收入水平等等。每个属性对应一个不同的因子向量y_a ∈ R^f，通过用户关联的属性集合来描述一个用户：

\sum_{a\in A(u)}y_a

矩阵分解模型应该整合所有的信号来源，并提升用户的表示能力：

\hat{r}_{ui}=\mu+b_i+b_u+q^T_i[p_u+|N(u)|^{-0.5}\sum_{i\in N(u)}x_i+\sum_{a\in A(u)}y_a]

尽管前面的例子涉及增强用户表示（在这种情况下数据缺乏更为普遍），但当需要时，物品也可以得到类似的处理。

时间动态

到目前为止，所介绍的模型都是静态的。实际上，产品的认知和受欢迎程度不断变化，随着新的选择的出现。同样，顾客的倾向也在演变，导致他们重新定义自己的口味。因此，系统应该考虑反映用户与物品交互的动态、随时间漂移的时间效应。

矩阵分解方法非常适合建模时间效应，可以显著提高准确性。将评分分解为不同的项使系统能够单独处理不同的时间方面。具体而言，以下项随时间变化：物品偏差b_i(t)、用户偏差b_u(t)和用户偏好p_u(t)。

第一个时间效应涉及到物品的受欢迎程度可能随时间变化。例如，电影的受欢迎程度可能因为外部事件（比如演员出现在新电影中）而上下波动。因此，这些模型将物品偏差b_i视为时间的函数。第二个时间效应允许用户随时间改变其基准评分。例如，一个倾向于给一部普通电影评分“4星”的用户现在可能给这样的电影评分“3星”。这可能反映了多种因素，包括用户评分标准的自然漂移、用户相对于其他近期评分的评分赋值，以及评分者在一个家庭中的身份随时间变化。因此，在这些模型中，参数b_u是时间的函数。

时间动态不仅仅影响物品的受欢迎程度和用户的基准评分，还影响用户的偏好以及用户与物品之间的互动。用户的偏好随时间变化。例如，一个心理惊悚片的粉丝可能一年后成为犯罪剧的粉丝。同样，人们对某些演员和导演的看法也会改变。模型通过将用户因子（向量p_u）作为时间的函数来考虑这种效应。另一方面，模型指定静态的物品特征q_i，因为与人不同，物品的性质是静态的。

精确的时间变化参数化会导致用时间动态预测规则替换方程4，用于在时间t时的评分预测：

\hat{r}_{ui}(t)=u+b_i(t)+b_u(t)+p_u(t)

具有不同置信水平的输入

在某些情况下，不是所有观察到的评分都应被赋予相同的权重或置信度。例如，大规模的广告可能会影响某些物品的评分，这些评分可能不准确地反映了长期特征。同样，系统可能面临敌对用户的干扰，他们试图操纵某些物品的评分。

另一个例子是建立在隐式反馈上的系统。在这种系统中，通过解读用户的持续行为，很难精确量化用户的偏好水平。因此，系统使用更粗糙的二元表示，即要么表示“可能喜欢该产品”，要么表示“可能对该产品不感兴趣”。在这种情况下，附加置信度分数到估计的偏好是有价值的。置信度可以源自可用的数字值，用于描述行为的频率，例如用户观看某个节目的时间或用户购买某个物品的频率。这些数字值表示了每个观察的置信度。与用户偏好无关的各种因素可能引起一次性事件；然而，重复事件更有可能反映用户意见。

阵分解模型可以轻松接受不同的置信水平，从而使其对不太有意义的观察结果给予较低的权重。如果观察到r_{ui} 的置信度表示为c_{ui} ，那么模型会修改成本函数（方程5），以考虑置信度的影响，如下所示：

\min_{p*,q*,b*}
\sum_{(u,i)\in  κ}c_{ui}(r_{ui}-\mu-b_u-b_i-q^T_ip_u)^2+\lambda(||q_i||^2+||p_u||^2+b_u^2+b_i^2)

有关涉及此类方案的实际应用的信息，请参阅《用于隐式反馈数据集的协同过滤》。

Netflix Prize竞赛

在2006年，在线DVD租赁公司Netflix宣布了一项竞赛，旨在改进其推荐系统。为了实现这一目标，该公司发布了一个训练集，其中包含超过1亿条评分数据，涵盖了约50万个匿名用户对超过17,000部电影的评分，每部电影的评分范围是1到5颗星。参与的团队需要提交对大约3百万条评分的测试集的预测评分，Netflix根据保留的真实评分计算均方根误差（RMSE）。如果有团队能够将Netflix算法的RMSE性能提高10%或更多，他们将赢得100万美元的奖金。如果没有团队达到10%的目标，Netflix将在每年的竞赛结束后向排名第一的团队颁发5万美元的进展奖。

该竞赛在协同过滤领域引起了轰动。在此之前，公开可用的协同过滤研究数据规模较小。这份数据的发布和竞赛的吸引力激发了大量的热情和活动。根据竞赛网站（www.netflixprize.com）的数据显示，来自182个不同国家的48,000多个团队已经下载了这些数据。

我们团队的参赛作品最初被称为BellKor，在2007年夏季夺得了竞赛的冠军，并以当时最好的成绩赢得了2007年的进展奖：比Netflix高出8.43％。后来，我们与Big Chaos团队合作，以9.46％的成绩赢得了2008年的进展奖。截至目前为止，我们仍然排名第一，逐渐接近10％的里程碑。

我们获胜的作品包括100多个不同的预测器集合，其中大多数是使用本文描述的方法的各种变体的因子分解模型。我们与其他顶级团队的讨论以及在公开竞赛论坛上的帖子表明，这些方法是最受欢迎和成功的用于预测评分的方法。

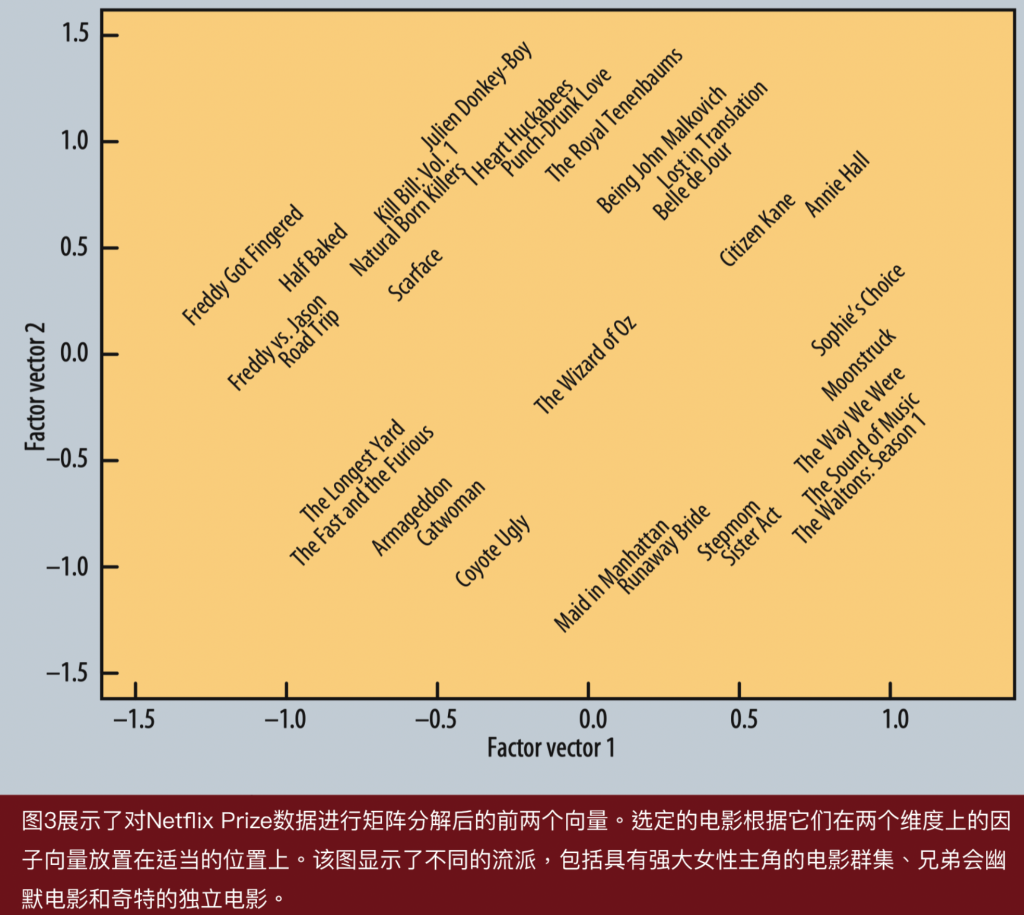
通过对Netflix用户-电影矩阵进行因子分解，我们可以发现预测电影偏好的最具描述性的维度。我们可以从矩阵分解中识别出前几个最重要的维度，并探索电影在这个新空间中的位置。图3展示了Netflix数据矩阵分解的前两个因子。电影根据它们的因子向量进行排列。熟悉这些电影的人可以在潜在因子中看到明显的含义。第一个因子向量（x轴）的一侧是面向男性或青少年观众的低俗喜剧和恐怖电影（Half Baked, Freddy vs. Jason），而另一侧则是带有严肃含义和强烈女性主角的戏剧或喜剧（Sophie’s Choice, Moonstruck）。第二个因子化轴（y轴）的顶部是独立的、备受好评的、古怪的电影（Punch-Drunk Love, I Heart Huckabees），而底部是主流公式化的电影（Armageddon, Runaway Bride）。在这些边界之间存在有趣的交叉点：在左上角，独立电影与低俗电影相遇，有Kill Bill和Natural Born Killers，这两部艺术电影涉及暴力主题。在右下方，严肃的女性主导电影与主流受众喜爱的电影相遇，有The Sound of Music。而在中间，吸引所有类型观众的是The Wizard of Oz。

在这个图中，一些相邻的电影通常不会被放在一起。例如，Annie Hall和Citizen Kane就靠在一起。尽管它们在风格上非常不同，但它们作为备受推崇的经典电影，由知名导演执导，有很多共同之处。事实上，因子分解中的第三个维度确实将它们分开。

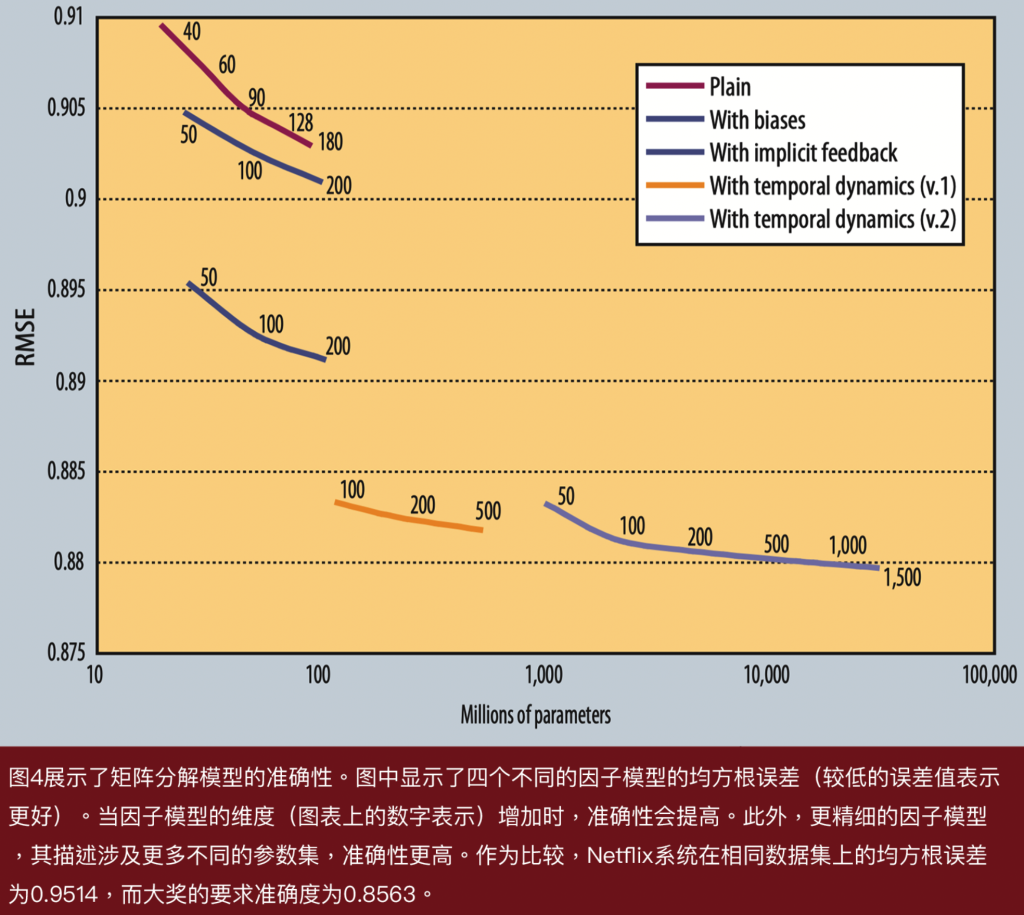
我们尝试了许多不同的因子分解实现和参数化方法。图4展示了不同模型和参数数量如何影响均方根误差（RMSE），以及因子分解不同实现的性能，包括简单的因子分解、添加偏差、使用隐性反馈增强用户配置文件，以及两种添加时间成分的变体。每个因子模型的准确性都随着涉及的参数数量增加而提高，这等效于增加因子模型的维度，图表中的数字表示维度的大小。

更复杂的因子模型，其描述涉及更多不同的参数集，更准确。事实上，时间成分特别重要，因为数据中存在显著的时间效应。

矩阵分解技术已成为协同过滤推荐系统中主要的方法学。对Netflix Prize数据等数据集的经验表明，它们提供比传统最近邻技术更高的准确性。同时，它们提供了一种紧凑的、内存高效的模型，系统可以相对容易地进行学习。更方便的是，这些技术还可以自然地集成许多关键的数据方面，如多种形式的反馈、时间动态和置信度水平。