半张量积(Semi-tensor product,STP)
一、半张量积于概念
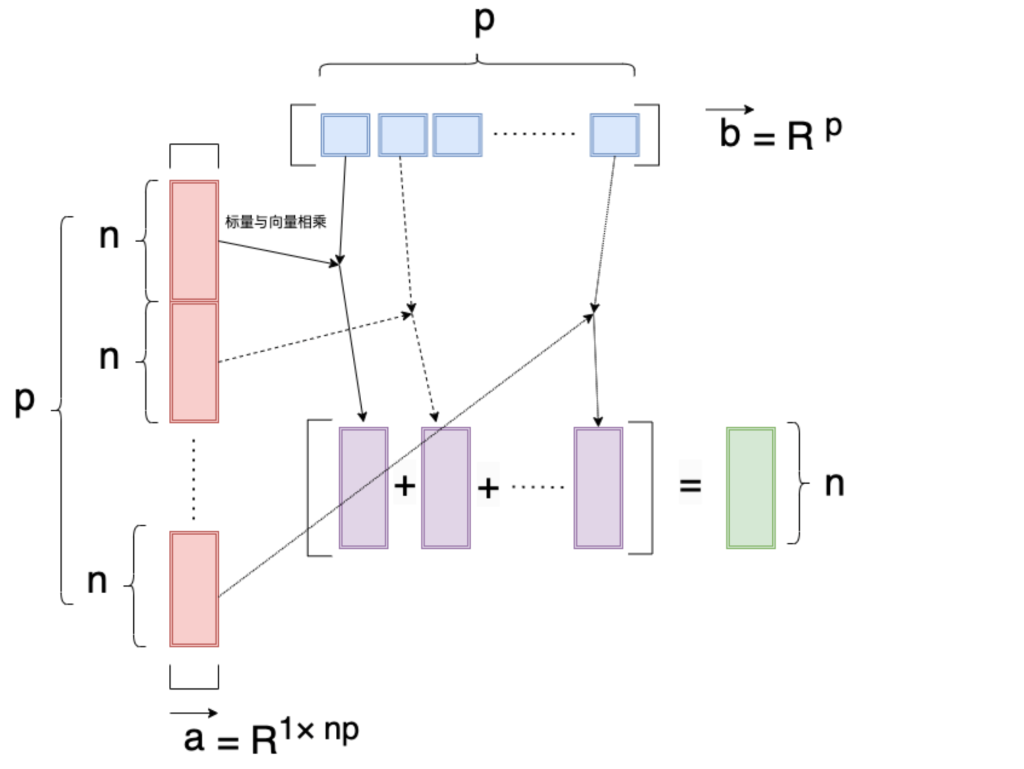
半张量积(Semi-tensor product,STP)是传统矩阵乘积[5]的一种泛化形式,其中因子矩阵可以具有任意维度。在本文中,我们着重研究了当左矩阵的列数与右矩阵的行数成比例时的情况,这被称为左半张量积。设a ∈ \R^ {1×𝑛𝑝}表示一个行向量(那么每一个向量长度就是n),设b ∈ \R^𝑝 ;那么 a 可以被均等地分割成 𝑝 个相等大小的块,即 a₁, a₂, ..., a_𝑝,左半张量积以 ⋉ 符号表示如下:
a ⋉ b = \sum^p_{i=1}a^ib_i \in\R^{1 \times n}\\
b^T ⋉ a^T = \sum^p_{i=1} b_i(a^i)^T \in\R^{n}
由图形化如下:
更一般的情况:
对于两个矩阵 A 和 B:
A ∈ \R^{𝐻×𝑛𝑃}, B ∈ \R^{𝑃 ×𝑄}
STP的定义如下:
C = A ⋉ B
其中 C ∈ \R^{1×𝑛} 可以由以下公式表示:
C = Σ_{𝑝,𝑖}=\sum_{𝑝,𝑖} a_𝑖 b_𝑖 ∈ \R^{1×𝑛}
C 包括了 𝐻 × 𝑄 个块,每个块 C_{ℎ𝑞} 可以按照以下方式计算:
C_{ℎ𝑞} = A(ℎ, :) ⋉ B(:, 𝑞 )
其中 A(ℎ, : ) 表示 A 中的第 ℎ 行,B(:, 𝑞 ) 表示 B 中的第 𝑞 列。
矩阵 C 包括了 𝐻 × 𝑄 个块,每个块 C^{hq} 的形状是 (1, 𝑛)。因此,整个矩阵 C 的形状应该是 (𝐻 , 𝑄, 𝑛)。
二、论文OD-Rec中的解释
论文:《On-Device Next-Item Recommendation with Self-Supervised Knowledge Distillation》中的4.2翻译
4.2 模型压缩
很显然,项目嵌入表占据了总可学习参数的绝大部分。压缩嵌入表是实现设备端推荐的关键。因此,我们首先采用张量列车分解(TTD)[13, 25]来缩小项目嵌入的大小。为了将嵌入表因子分解为 i 个较小的张量,我们让项目总数为|𝑉 | = \prod^𝑑_{𝑘=1}𝐼_𝑘 ,嵌入维度 𝑁 = \prod^𝑑_ {𝑘=1} 𝐽_𝑘 。对于一个特定的项目 𝑣,其索引为 𝑖,我们根据 [13] 将行索引 𝑖 映射为 𝑑 维向量 𝑖 = (𝑖_1 , ...,𝑖_𝑑 ),然后从 TT-核心中获取索引的特定切片来在切片上执行矩阵乘法 ( 参见公式(1) )。通过这种分解,模型不需要存储消耗大量内存的嵌入表。相反,我们只需存储 TT-核心以实现对嵌入表中条目的近似,即一系列小张量的乘法。假设给定尺寸为 \sum^𝑑_{𝑘=1} 𝑅_{𝑘−1} 𝐼_𝑘 𝐽_𝑘 𝑅_𝑘的 {G_𝑘},压缩率为:
rate=\frac{\prod_{k=1}^{d}I_kJ_k}{I_1J_1R+\sum_{k=1}^{d-1}I_jJ_k\frac{R^2}{n^2}+I_dJ_d\frac{R}{n^2}}
其中,𝑅_0 = 𝑅_𝑑 = 1。为简单起见,我们在本文中将相同的秩 𝑅 分配给中间的 TT-核心,即,\{𝑅_𝑘 \}^{𝑑−1}_{𝑘=2} = 𝑅。
然而,传统的TT分解要求因子之间具有严格的维度一致性,可能导致维度冗余。例如,如果我们将项目嵌入矩阵分解为两个较小的张量,即 X = G₁ G₂,以获取每个项目的嵌入,那么 G₁ 的列数应该与 G₂ 的行数相同。这种一致性约束对于灵活高效的张量分解来说过于严格,阻碍了对嵌入表进一步压缩的过程。因此,受到 [54] 的启发,我们提出将半张量积与张量列车分解相结合,其中 TT-核心的维度可以任意调整。传统的 TT-核心之间的张量积被半张量积所取代,如下所示:
X = \hat{G}_1⋉\hat{G}_2⋉···⋉\hat{G}_d
其中 \{G_𝑘\}^𝑑_{𝑘=1} 是在应用基于半张量积的张量列车分解 (STTD) 后得到的核心张量,而 G_1 ∈ \R^{𝐼_1 𝐽_1×𝑅} ,\{G_k\}^{𝑑-1}_{k=2} ∈ \R^{\frac{𝑅}{𝑛} × \frac{𝐼_𝑘 𝐽_𝑘}{n}×𝑅} ,以及 G_𝑑 ∈ \R^{\frac{𝑅}{𝑛}×\frac{𝐼_𝑑 𝐽_𝑑}{n}}。
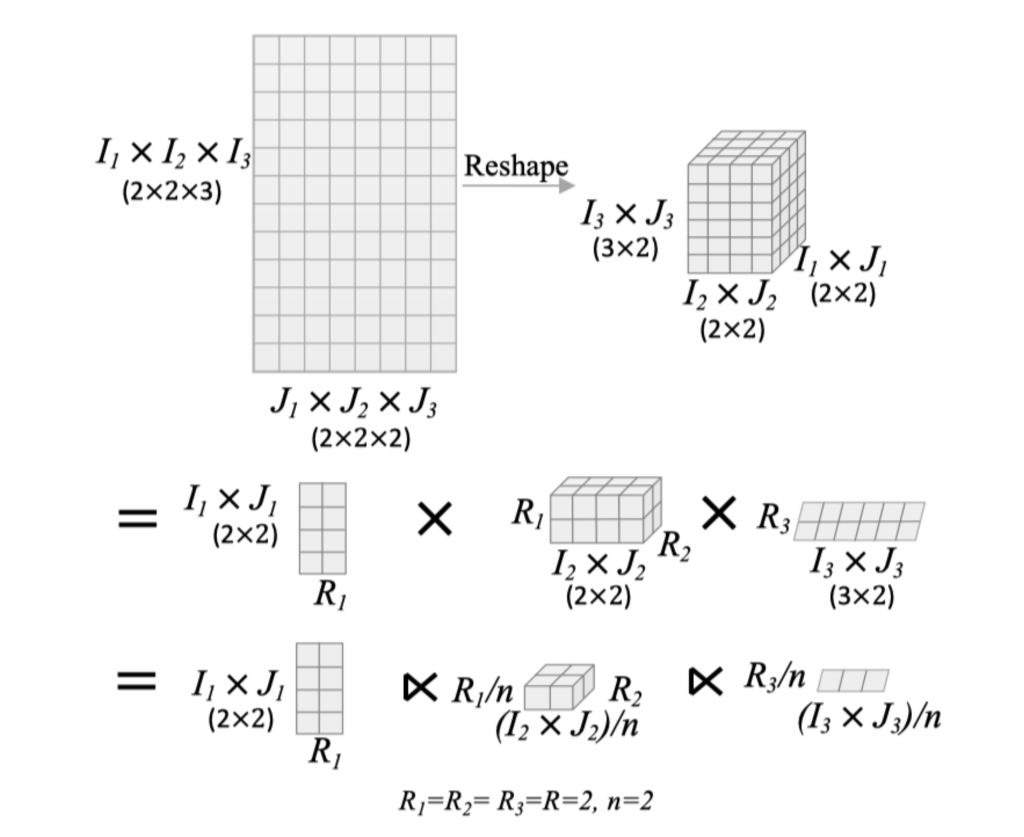
结合图2我们可以知道,我们将原来的user-item的embedding矩阵给他reshape为三维矩阵,原先我们是通过普通的TT分解,就可以得到第二行的形式,他形状计算如下:
\R^{12,8}\stackrel{Reshape}{=}\R^{4,4,6}=\R^{4,2} \times \R^{2,4,2} \times \R^{2,6}
而我们结合了STP后有
\R^{12,8}\stackrel{Reshape}{=}\R^{4,4,6}=\R^{4,2} ⋉ \R^{1,2,2} ⋉ \R^{1,3}
论文中G_1 ∈ \R^{𝐼_1 𝐽_1×𝑅} ,\{G_k\}^{𝑑-1}_{k=2} ∈ \R^{\frac{𝑅}{𝑛} × \frac{𝐼_𝑘 𝐽_𝑘}{n}×𝑅} ,以及 G_𝑑 ∈ \R^{\frac{𝑅}{𝑛}×\frac{𝐼_𝑑 𝐽_𝑑}{n}}。
以G_1 和 G_2 举例,这里给出了两个核心张量的维度:
G_1 \in \mathbb{R}^{I_1J_1 \times R}G_2 \in \mathbb{R}^{\frac{R}{n} \times \frac{I_2J_2}{n} \times R}
这两个张量可以通过半张量积(Semi-tensor product, STP)进行运算。
首先,我们回顾一下半张量积的定义:
对于两个矩阵 (A \in \mathbb{R}^{m \times n}) 和 (B \in \mathbb{R}^{p \times q}),它们的半张量积 (C = A ⋉ B) 定义如下:
C = \sum_{i=1}^{p} a_i \cdot b_i \in \mathbb{R}^{m \times q}
其中 (a_i) 和 (b_i) 是矩阵 (A) 和 (B) 中的列向量。
现在,我们将它应用到 (G_1) 和 (G_2) 中:
- 对于 (G_1) 和 (G_2),它们的半张量积运算如下:
C = G_1 ⋉ G_2
-
具体地,(
G_1) 的维度为 (I_1J_1 \times R),(G_2) 的维度为 (\frac{R}{n} \times \frac{I_2J_2}{n} \times R)。对于单个区块有C_{ijk}=G_1(i,:)⋉G_2(:,j,k)
其中,`$$i$$`取值范围为 `$$I_1,J_1$$` ; `$$j$$`取值范围为 `$$\frac{I_2J_2}{n}$$` ;`$$k$$` 取值范围为`$$R$$`
```katex
G_1(i,:)\in \R^{1 \times R} \\
G_2(:,j,k)\in \R^{\frac{R}{n} \times 1\times1} \\
C_{ijk} \in \R^n
for i in I1J1:
for k in R:
for j in (I2J2)/n:
# 每一个有n维度所以,半张量积运算后,结果张量 (`$$C$$`) 的维度将为 (`$$I_1J_1 \times I_2J_2 \times R$$`)。
同理 ,
X = C ⋉ G_3
对于单个区块有
X_{ijk}=C(i,j,:)⋉G_3(:,k)
C(i,j,:) \in \R^{R}\\
G_3(:,k) \in \R^{\frac{R}{n}}\\
X_{ijk}\in \R^n
for i in I1J1:
for k in I2J2:
for j in (I3J3)/n:
# 每一个有n维度所以最后结果:
X \in \R^{I_1J_1 \times I_2J_2 \times I_3J_3}
留言