(1) KL散度
熵(Entropy)是一个基本概念,用于衡量随机变量的不确定性或信息量。熵越高,表示随机变量的不确定性越大,信息量也就越大。
KL散度,也称为相对熵(Relative Entropy)是用来衡量两个概率分布直接差异的方式,它衡量了两个概率分布之间的差异或者说是信息损失。
给定两个离散概率分布P和Q,KL 散度的定义如下:
D_{KL}(P \| Q) = \sum_{x} P(x) \log\left(\frac{P(x)}{Q(x)}\right)
KL 散度是用来衡量两个概率分布之间的差异或信息损失的度量。
D_{KL}(P \| Q) = \sum_{x} P(x) \log\left(\frac{P(x)}{Q(x)}\right)\\
=\sum_x [P(x)log(P(x))-P(x)log(Q(x))]\\
令
G(P) = \sum_{x} P(x) \log(P(x))
H(P, Q) = -\sum_{x} P(x) \log(Q(x))
所以公式(2)则为
D_{KL}(P \| Q) =G(P)+H(P,Q)
对于第一部份G(P)可以自己对于自己的差异衡量,而在训练之中,P是训练的数据集,训练集是固定的,他的分布也是固定的。也就是说,由KL散度的定义来讲,他的意义是他本身对于概率恒定为1的差异。所以他是一个常数的值。而第二部分的H(P,Q)是变化的,因为他含有训练模型的预测Q,所以他是变化的。也就是说我们可以通过最小化H(P,Q)来让Q(x)达到与P(x)分布最小的差异。
而第二部分H(P,Q)我们称之为交叉熵,其来源与信息论中的交叉熵一样
f(x)=-\int p(x)log\ g(x)dx
其注意,交叉熵是一个非对称的度量,即H(P, Q) ≠ H(Q, P)。
(2)多分类交叉熵与单分类交叉熵
我们可以看见两个形式的交叉熵函数如下:
L_{mul} = \frac{1}{N}\sum_{i} L_i = - \frac{1}{N}\sum_{i} \sum_{c=0}^My_{ic}\log(p_{ic})
c是类别,y_{ic}表示这里表示当i是c类的时候为1,否则为为0。p_{ic}表示i是c的概率。
L_{log}(y,p)=-[ylog(p)+(1-y)log(1-p)]
在許多博客之中都是先說(8)再說(7),我認為這是不符合邏輯的。我認為,(8)是由(7)所推導出來的。當L_{mul}為二分類的時候,也就是說,c的取值只有可能為0和1,當為0的時候,i的取值可能為0或者1,則有
L_{mul}|\{c=0\} = -1/N [y_{00}log(p_{00})+[y_{10}log(p_{10})]]=-1/N\ y_{00}log(p_{00})\\
L_{mul}|\{c=1\} = -1/N [y_{01}log(p_{01})+[y_{11}log(p_{11})]]=-1/N\ y_{11}log(p_{11})\\
L_{mul}=L_{mul}|\{c=0\}+L_{mul}|\{c=1\}=-1/N[y_{00}log(p_{00})+y_{11}log(p_{11})]
由於是二分類,所以p_{00}和p_{11}是對立事件,令p_{00}=p,則p_{11}=1-p,y同理。
所以可以推出
L_{mul}=L_{mul}|\{c=0\}+L_{mul}|\{c=1\}=-1/N[y_{00}log(p_{00})+y_{11}log(p_{11})]\\
=-[ylog(p)+(1-y)log(1-p)]
(3) softmax的导数
我们对于softmax的结构有如下:
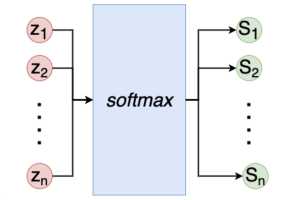
softmax 公式如下:
S_i=\frac{e^{z_i}}{\sum_k^ne^{z_k}}
其中,z是最后的全连接层的输出,z_i表示第i个单元的输出
\frac{\partial S_i}{\partial z_j}=
\frac{
\partial(\frac{e^{z_i}}{\sum_k^ne^{z_k}})
}{
\partial z_j
}\\
=\frac{
\frac{\partial e^{z_i}}{\partial z_j}· \sum_k^n e^{z_k}
-
e^{z_i}·e^{z_j}
}{
[\sum_k^n e^{z_k}]^2
}
这里i和j并不一定是一样的,所以我们需要分情况讨论
1′. 若i = j 有
\frac{\partial S_i}{\partial z_i}=\frac{
\frac{\partial e^{z_i}}{\partial z_i}· \sum_k^n e^{z_k}
-
e^{z_i}·e^{z_i}
}{
[\sum_k^n e^{z_k}]^2
}\\
=
\frac{
e^{z_i} · \sum_k^n e^{z_k}
}{
[\sum_k^n e^{z_k}]^2
}-
\frac{
[e^{z_i}]^2
}{
[\sum_k^n e^{z_k}]^2
}\\=
\frac{
e^{z_i}
}{
\sum_k^n e^{z_k}
}-
[\frac{
e^{z_i}
}{
\sum_k^n e^{z_k}
}]^2\\
=s_i-s_i^2
2′. 若i \not= j 有
\frac{\partial S_i}{\partial z_i}=
\frac{
\frac{\partial e^{z_i}}{\partial z_j}· \sum_k^n e^{z_k}
-
e^{z_i}·e^{z_j}
}{
[\sum_k^n e^{z_k}]^2
}\\
=
\frac{
0· \sum_k^n e^{z_k}
-
e^{z_i}·e^{z_j}
}{
[\sum_k^n e^{z_k}]^2
}\\
=-
\frac{
e^{z_i}
}{
\sum_k^n e^{z_k}
}·
\frac{
e^{z_j}
}{
\sum_k^n e^{z_k}
}\\
=-s_i·s_j
綜上
\frac{\partial S_i}{\partial z_j}=
\begin{cases}
s_i-s_i^2 &i=j\\
-s_i s_j& i \not= j
\end{cases}
(4) 交叉熵結合softmax的导数
交叉熵结合softmax的网络结构如下:
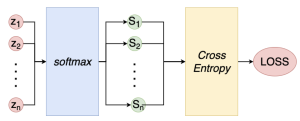
\frac{\partial C}{\partial z_i}=\sum_j^n \frac{\partial C}{\partial S_j} \frac{\partial S_j}{\partial z_i}\\
= \sum_j^n {
\frac{\partial(-\sum^n_k y_k log(S_k))} {\partial S_j}·
\frac{\partial S_j}{\partial z_i}
}
当k\not=j有
\frac{\partial(-\sum^n_k y_k log(S_k))} {\partial S_j}=0
当k=j有
\frac{\partial(-\sum^n_k y_k log(S_k))} {\partial S_j}=-\frac{y_j}{s_j}
所以,公式(19)可以推导为如下:
(19)=-\sum_j^n \frac{y_j}{s_j}· \frac{s_j}{z_i}\\
=-[\frac{y_i}{s_i}·(s_i-(s_i)^2)+\sum_{i\not=j}^n \frac{y_j}{s_j}(-s_i s_j)] \\
=-[y_i - y_i s_i -\sum_{i\not=j}^n y_j s_i]\\
=-[y_i -\sum_{j=1}^n y_j s_i]\\
=-[y_i -s_i\sum_{j=1}^n y_j] )\\
=s_i-y_i
其中,第二行带入了公式(18),第5行是因为y是one-hot 或者在KD中softmax(T),所以总和为1。所以最后的求导结果为预测结果减去标签。
(5)推导KD论文中公式(2)-(4)
soft labels 的损失函数如下:
L_{soft}=-\sum_j^N t_j log(s_i)
其导数为
\frac{\partial L_{soft}}{\partial z_i}
= \frac{\partial [-\sum_j^N t_j log(s_i)]}{\partial (Z_i/T)}\frac{\partial (Z_i/T)}{z_i}\\
= \frac{1}{T}(s_i-t_i)\\
= \frac{1}{T}(\frac{e^{z_i/T}}{\sum_k^ne^{z_k/T}}-\frac{e^{v_i/T}}{\sum_k^ne^{v_k/T}})
由泰勒公式可得
\lim_{T \to \infty }e^{z_i/T} = 1+z_i/T
所以带入(23)有
\lim_{T \to \infty }\frac{\partial L_{soft}}{\partial z_i} =
\frac{1}{T}(\frac{1+z_i/T}{N+\sum_k^nz_k/T}-\frac{1+v_i/T}{N+\sum_k^nv_k/T})
假設\sum z_i =0並且\sum v_i =0
If we now assume that the logits have been zero-meaned separately for each transfer case so that ∑ j z j = ∑ j v j = 0 Eq. 3 simplifies to:
\lim_{T \to \infty }\frac{\partial L_{soft}}{\partial z_i} =
\frac{1}{T}(\frac{1+z_i/T}{N}-\frac{1+v_i/T}{N}) =
\frac{1}{NT}[(1+z_i/T)-(1+v_i/T)] =
\frac{1}{NT^2}[z_i-v_i]
因为在高温极限下,对于指数函数的近似计算中,e^{z_i/T} 和 e^{v_i/T} 中的 1/T 部分将迅速趋近于 1,从而导致它们的比例变得与温度 T 无关。这意味着分母中的 N + \sum_k^n z_k/T 和 N + \sum_k^n v_k/T 部分也趋近于 N,在高温极限下,它们的值对结果的影响会减弱。
在这种情况下,导数的极限 \lim_{T \to \infty }\frac{\partial L_{soft}}{\partial z_i} 可以简化为:
\lim_{T \to \infty }\frac{\partial L_{soft}}{\partial z_i} =
\frac{1}{T}(\frac{1+z_i/T}{N}-\frac{1+v_i/T}{N}) =
\frac{1}{NT}[(1+z_i/T)-(1+v_i/T)] =
\frac{1}{NT^2}[z_i-v_i]
在高温下,即温度参数 T 趋近于无穷大时,soft labels 损失函数的导数趋近于 1/2(z_i - v_i)^2 这是因为指数函数和分母的近似行为。
在推导过程中,我们使用了泰勒公式:
\lim_{T \to \infty} e^{z_i/T} = 1 + \frac{z_i}{T}
当温度 T 非常大时,分母的指数函数项 \frac{e^{z_i/T}}{\sum_k^n e^{z_k/T}} 和 \frac{e^{v_i/T}}{\sum_k^n e^{v_k/T}} 都会接近于1。这是因为指数函数在分母中的分子项在无穷大的 T 值下会趋近于1,同时分母中的所有指数项也会趋近于1。这就使得 soft labels 损失函数的导数在高温下趋近于:
\frac{1}{T} \left(1 - 1\right) = 0
然而,在接近于无穷大的情况下,泰勒公式会导致项 1+z_i/T 和 1+v_i/T 中的线性项逐渐减小,从而损失函数的导数会趋近于二次项 1/2(z_i - v_i)^2。这就解释了在高温下为什么 soft labels 损失函数的导数会趋近于 1/2(z_i - v_i)^2。
留言