矩阵分解

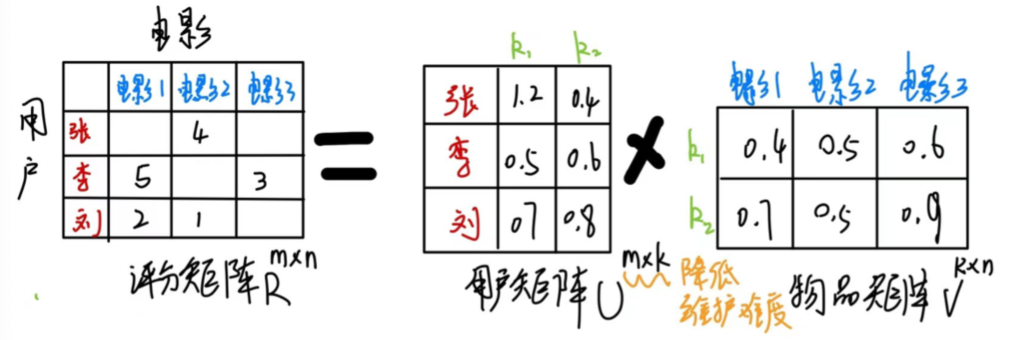
推荐算法要预测用户所没有看过的东西的评分，为了能够预测用户的评分，我们需要构建两个矩阵U、V，通过构建的两个矩阵U、V来预测User-Item矩阵的空缺部分，也就是矩阵R中空的。其中U、V分别代表用户、物品的特征(feature)，通过某一个用户的向量与某一个物品向量做内积从而得出该用户对这个物品的偏好程度。而核心问题就转化到了我们如何构建一个U和V来能够最大程度拟合用户之特征。

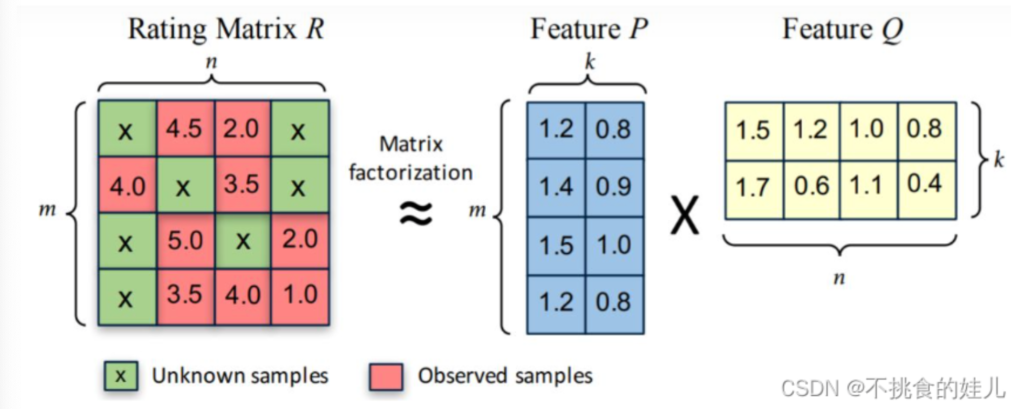
对于如上图，矩阵分解算法将m \times n 维的矩阵R分解为m \times k的用户矩阵P和 k \times n维的物品矩阵Q相乘的形式。其中m为用户的数量， n为物品的数量，k为隐向量（Latent Factor）的维度。 k是超参数。

将两个矩阵相乘，就可以得到一个满秩的矩阵R。那么，我们就对未被评价过的物品，有了一个预测评分。接下来，可以将评分进行排序，推荐给用户。这就是矩阵分解对于推荐系统最基本的用途。矩阵R第u行第i列的元素，可以表示第u个人对第i个item的兴趣程度。

将现有的稀疏矩阵R分解为两个矩阵，k为隐向量，k的长度是所选取的特征长度，也是一个超参数。在分解完成两个矩阵后，我们就需要学习U和V的k向量，让他更好的匹配R矩阵。

矩阵分解的目的: 通过分解之后的两矩阵内积，来填补缺失的数据，用来做预测评分。 通过机器学习的手段将用户行为矩阵中缺失的数据(用户没有评分的元素)填补完整，最终达到可以为用户做推荐的目标。

特征值分解

A为n阶矩阵，有如下公式

A\alpha = \lambda \alpha

则\alpha 是特征向量、\lambda 是特征值

于是我们有

A=QΣQ

Q是特征向量。Σ是对角矩阵，对角线上是矩阵A的由大到小排列的特征值，他们顺序代表着对矩阵Q变化方向的重要程度，利用前N个值就可以得到接近这个矩阵的变化，从而提取这个矩阵最重要的特征，比如下面的考研典型题目：

奇异值分解

对于一个m \times n矩阵M，有

M=UΣV^T

其中 U是m \times n的正交矩阵， V 是 n \times n的正交矩阵， \Sigma是m \times n的对角矩阵。 Σ对角线上的元素就称为M的奇异值.

分解后， U矩阵为6 \times 6的正交矩阵, V为4 \times 4的正交矩阵。 S为对角矩阵即公式中的\Sigma。选取S中较大的k个元素作为隐含特征。删除S的其他维度以及 U和 V对应的维度，矩阵分解就完成了。

Funk-SVD

直接通过训练集中的观察值利用最小化RMSE学习用户特征矩阵P和物品特征矩阵Q，挖掘用户的潜在特征矩阵P和物品潜在特征矩阵Q来估计评分

R≈P \times Q 

在求出了P、Q后，我们则有

r_{ij}=p_iq_j^T=\sum_{k=1}^K p_{ik}q_{kj}

所以优化目标为

argmin \sum_{i,j}(r_{ij}-p_iq_j)^2+(||p_i||+||q_j||)