[学习笔记]矩阵乘积态Tensor Train Decomposition 与代码实现

一、矩阵乘积态与Tensor-Train 分解

1.1 矩阵乘积态与Tensor-Train 概念

矩阵乘积态（Matrix Product State，简称MPS）是一种用于表示量子多体系统的方法，特别在量子信息、量子计算和凝聚态物理领域中得到广泛应用。它是一种张量网络的表示方法，用于描述量子态以及其演化过程。

Tensor Train分解是一种用于分解多维张量的方法，类似于矩阵分解，但适用于更高维度的数据。它将一个多维张量分解成一系列的小块（或称为核），每个小块是一个低秩张量，它们相互连接组成一个网络。这种分解允许高效地表示和操作高维数据，同时保留了重要的数据结构和特征。

阵乘积态主要应用于量子物理领域，用于描述量子态的性质和演化，而Tensor-Train 分解更广泛地应用于机器学习、数值计算等领域，用于处理高维数据的表示和计算。

\varphi_{s_0s_1···s_{N-1}}=\sum_{\{a_*\}} \prod_n^{N-1}A^{(n)}_{a_ns_na_{n+1}}I_{a_0a_N}\\
=\sum_{\{a_*\}}A^{(0)}_{a_0s_0a_1} A^{(1)}_{a_1s_1a_2}···A^{(N-2)}_{a_{N-2}s_{N-2}a_{N-1}}A^{(N-1)}_{a_{N-1}s_{N-1}a_{N}}

其中，

• \varphi \in \R^{s_0 \times s_1 ···\times s_{N-1}} 是一个 N 阶张量，表示被分解的矩阵。它的每一个索引 s_i 对应于该张量在第 i 个维度上的index。N 表示该张量的阶数，即它有多少个维度。
• \{a_*\} 是一组索引，表示在张量乘法的过程中，每个小张量核 A^{(n)} 和 I 所连接的方式。
• A^{(n)}_{a_ns_na_{n+1}} 是一个三维张量，其中 n 是索引，a_n，s_n 和 a_{n+1} 是张量在不同维度上的索引。这些维度有特定的尺寸，其中 \chi 是一个参数，用于控制张量核的秩（rank）。
• A_{a_ns_na_{n+1}}\in \R^{\chi \times d \times \chi} ,其中,d是物理维度,\chi 是虚拟维度（关系到了我们需要压缩的系数）
• d 表示每个维度有多少数据
• N 表示张量的阶数，即它有多少个维度。

从维度方面看待，维度的变化如下：

\R^{d^N}=\R^{
[(1 \times d \times \chi)\times (\chi \times d \times \chi)···  (\chi \times d \times 1)]
}

也就是说，从原来的单一的\R^{d^N} 分解到N-2个\R^{\chi \times d \times \chi} 和 \R^{1 \times d \times \chi} 和一个\R^{\chi \times d \times 1}的矩阵

1.2 为什么它可以压缩？

我们假设她的物理维度为d ,虚拟维度为\chi 则原来矩阵的空间复杂度为\varphi

(d \times d ··· d)\sim O(d^N)

而分解后的空间复杂度为A

2d\chi+(N-2)d\chi^2 \sim O(Nd\chi^2)

也就是说，通过分解我们将空间复杂度从O(d^N) 降到 O(Nd\chi^2) ,当\chi 一定时，存储的空间复杂度从指数级别降低到线性级别，而有了A我们就可以得到\varphi 所以就达到了压缩的目的。

1.3 图形化表示乘积态

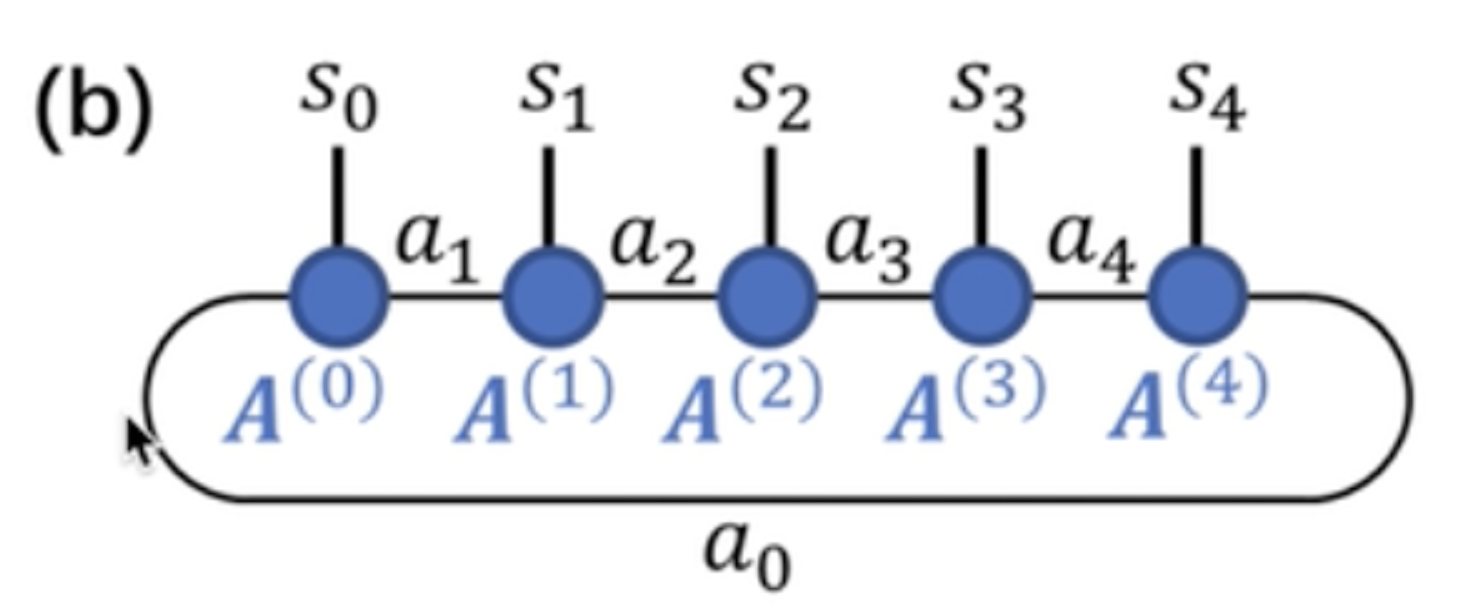
这个图像中，蓝色表示矩阵，其他符号表示指标。也就是说s_0 、 a_1 作用在A^{(0)} 上面，图形无法知道作用顺序，如上面是一个循环的乘积态，所以也称为闭边界。共同作用的指标是可以被消除的(爱因斯坦求和中的左边共有指标)，最后得到的是不可被消除的指标作用于最后结果之上(爱因斯坦求和中的右边部分)

二、中心正交化（Center Orthogonalization）

在张量网络表示中，特别是像Tensor Train（TT）和Matrix Product States（MPS）这样的方法中，张量之间的正交性对于高效表示和计算至关重要。中心正交化是一种将张量网络中的张量重新排列和变换的过程，以便使得一部分信息集中在某个核心（中心）张量中，从而提高表示的紧凑性。

在中心正交化过程中，一开始的张量被分解成一对正交张量，这一对张量分别代表了左边和右边的正交部分。这可以通过奇异值分解（Singular Value Decomposition，SVD）来实现。

对于一些特定的量子算法或数值模拟，正交化可以使计算过程更为高效。比如求二范式则可以求中心的二范式，大大提高效率。

2.1 奇异值分解法分解向量

2.1.1 奇异值分解概念

奇异值分解（Singular Value Decomposition，SVD）是一种常用于矩阵分解和降维的数学方法。给定一个矩阵 M，SVD 将其分解为三个矩阵的乘积：

M = U \Sigma V^\top

其中：

• U 是一个正交矩阵，其列向量称为左奇异向量。
• \Sigma 是一个对角矩阵，其对角线上的元素称为奇异值。奇异值是按照从大到小排列的。
• V 是另一个正交矩阵，其行向量称为右奇异向量。

在SVD分解中，通常将左奇异向量矩阵 U 和包含奇异值以及右奇异向量的矩阵 V^\top 合并到一起，得到一个紧凑的表示。

具体地，将奇异值矩阵 \Sigma 的非零元素按照从大到小排列，得到一个对角矩阵：

\Sigma = \begin{bmatrix}
\sigma_1 & 0 & 0 & \dots & 0 \\
0 & \sigma_2 & 0 & \dots & 0 \\
0 & 0 & \sigma_3 & \dots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \dots & \sigma_r \\
0 & 0 & 0 & \dots & 0 \\
\end{bmatrix}

其中 r 是矩阵 M 的秩，也是非零奇异值的数量。

然后，将左奇异向量矩阵 U 的前 r 列和右奇异向量矩阵 V 的前 r 行提取出来，形成矩阵 C 和矩阵 D：

C = U[:, :r]
\\D = \begin{bmatrix}
\sigma_1 & 0 & 0 & \dots & 0 \\
0 & \sigma_2 & 0 & \dots & 0 \\
0 & 0 & \sigma_3 & \dots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \dots & \sigma_r \\
\end{bmatrix} \cdot V^\top[:r, :]

这样，C 包含了矩阵 M 的主要信息，而 D 包含了奇异值和右奇异向量的信息。这种分解在很多应用中都非常有用，例如降维、数据压缩、矩阵近似等。

2.1.2 奇异值TT分解步骤

这对正交张量中的一部分被合并到一个中心张量中，同时保持原始张量的信息。这个过程不断迭代，逐步将信息从左右两侧集中到中心，从而达到中心正交化的目的。具体过程如下：

总体上可以归纳为以下几个步骤：

1. 初始化： 假设你有一个张量网络，其中的张量需要进行中心正交化。初始时，这些张量可能是任意排列的。

2. 奇异值分解（SVD）： 选择一个张量，将其分解为两个部分：一个正交的左张量和一个正交的右张量。

3. 合并到中心： 将其中一个正交张量合并到一个中心张量中。这个中心张量将会积累来自不同张量的信息，从而减少总体的表示复杂度。通常，这个中心张量会处于整个张量网络的中心位置。

4. 迭代： 重复上述步骤，选择下一个需要进行中心正交化的张量，并将其分解为正交左张量和右张量，然后将其中一个合并到中心张量中。这个过程会不断迭代，逐渐将信息从边缘的张量转移到中心张量中。

5. 收敛或截断： 在迭代过程中，你可以选择在某个步骤进行截断操作，即保留部分最重要的特征，丢弃一些较小的值，以减少计算和存储成本。截断后，继续进行迭代，直到整个张量网络足够接近中心正交的状态。

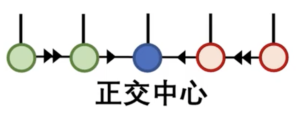
过程大概如下图所示

公式如下：

A^{(n)} \stackrel{SVD}{\rightarrow} \hat{A}^{(n)}SV\\

SV\rightarrow A^{n+1}

这样不断地重复，整体图如下

2.1.3 代码实现

向前传播

d是物理维度,\chi 是虚拟维度，length是分解的长度

中间维度是A_{a_ns_na_{n+1}}\in \R^{\chi \times d \times \chi}，头尾是A_{a_ns_na_{n+1}}\in \R^{1 \times d \times \chi}和A_{a_ns_na_{n+1}}\in \R^{\chi \times d \times 1}

import torch as tc

print('建立开放边界MPS')
length, d, chi = 6, 2, 4
dtype = tc.float64

#随机生成A
#第一个和最后一个个的头尾为1，
tensors = [tc.randn(1, d, chi, dtype=dtype)] + \
          [tc.randn(chi, d, chi, dtype=dtype)
           for _ in range(length-2)] + \
          [tc.randn(chi, d, 1, dtype=dtype)]

psi = tensors[0]
print('第0个张量的形状为：', tensors[0].shape)
for n in range(1, len(tensors)):
    print('第%d个张量的形状为：' % n, tensors[n].shape)
    #tensordot用来做通用维度的张量相乘，第一个第二个参数表示输入的张量，最后一个表示要计算的维度
    psi = tc.tensordot(psi, tensors[n], [[-1], [0]])
    print('收缩完该张量后，所得张量的形状为：', psi.shape)
psi = psi.squeeze()
print('去掉前后维数为1的指标得到最终的高阶张量，形状为：')
print(psi.shape)

第0个张量的形状为： torch.Size([1, 2, 4])
第1个张量的形状为： torch.Size([4, 2, 4])
收缩完该张量后，所得张量的形状为： torch.Size([1, 2, 2, 4])
第2个张量的形状为： torch.Size([4, 2, 4])
收缩完该张量后，所得张量的形状为： torch.Size([1, 2, 2, 2, 4])
第3个张量的形状为： torch.Size([4, 2, 4])
收缩完该张量后，所得张量的形状为： torch.Size([1, 2, 2, 2, 2, 4])
第4个张量的形状为： torch.Size([4, 2, 4])
收缩完该张量后，所得张量的形状为： torch.Size([1, 2, 2, 2, 2, 2, 4])
第5个张量的形状为： torch.Size([4, 2, 1])
收缩完该张量后，所得张量的形状为： torch.Size([1, 2, 2, 2, 2, 2, 2, 1])
去掉前后维数为1的指标得到最终的高阶张量，形状为：
torch.Size([2, 2, 2, 2, 2, 2])

分解向量

def ttd_tc(x, chi=-1, svd=True):
    """
    :param x: 被分解的张量
    :param chi: 维度裁剪. dc=None表示不裁剪，使用QR分解;
                如果裁剪则使用 SVD 分解 
    :param svd: use svd or qr
    :return tensors: tensors in the TT form
    :return lm: singular values in each decomposition (calculated when dc is not None)
    """
    #形状
    dims = x.shape
    #求数量
    ndim = x.ndimension()
    #记录第一维度的大小
    dimL = 1

    tensors = list()
    lm = list()
    if chi is None:
        chi = -1

    for n in range(ndim-1):
        if (chi < 0) and (not svd):  # 不裁剪
            #先reshape为前一个向量*维度，也就是说第一维度是有前面的n个向量*目前项链的个数
            q, x = tc.linalg.qr(x.reshape(dimL*dims[n], -1))
            dimL1 = x.shape[0]
        else:
            q, s, v = tc.linalg.svd(x.reshape(dimL*dims[n], -1))

            #print(q.shape,s.shape,v.shape)
            #torch.Size([4, 4]) torch.Size([4]) torch.Size([1024, 1024])

            #判断截取的长度不应该大于s的长度
            if chi > 0:
                dc = min(chi, s.numel())
            else:
                #向量个数
                dc = s.numel()

            #截取
            #左奇异值截取前dc列
            q = q[:, :dc]
            #截取前dc行
            s = s[:dc].to(q.dtype)
            #保存s
            lm.append(s)

            #右奇异值（s的前dc列的对角元素·v的前dc列）
            #print(s.shape,tc.diag(s).shape,v[:dc, :].shape)
            #torch.Size([4]) torch.Size([4, 1024])
            #diag表示把这列元素填充到对角线上
            #[4]-diag->[4,4]
            #[4,4]·[4,1024]--mm->[4,1024]

            #x是下一个大块
            x = tc.diag(s).mm(v[:dc, :])

            #print(s)
            #print(tc.diag(s))
            #print(x.shape)
            #torch.Size([dc, 1024]) or torch.Size([s.numel(),1024])

            #记录截取数值,为下一个dimL*dims[n]做准备
            dimL1 = dc
        #记录当前块
        tensors.append(q.reshape(dimL, dims[n], dimL1))
        #记录截取数值
        dimL = dimL1
    #记录最后一个
    tensors.append(x.reshape(dimL, dims[-1], 1))
    # tensors[0] = tensors[0][0, :, :]
    return tensors, lm
#这个函数把正交中心移动到最后一个

#设定维度
d = 4
x = tc.randn((d, d, d, d,d,d), dtype=tc.complex128)

tensors = ttd_tc(x,chi=-1)[0]
for n in range(len(tensors)):
    print('第%d个张量的维数为：' % n,
          tensors[n].shape)

第0个张量的维数为： torch.Size([1, 4, 4])
第1个张量的维数为： torch.Size([4, 4, 16])
第2个张量的维数为： torch.Size([16, 4, 64])
第3个张量的维数为： torch.Size([64, 4, 16])
第4个张量的维数为： torch.Size([16, 4, 4])
第5个张量的维数为： torch.Size([4, 4, 1])

def full_tensor(tensors):
    # 注：要求每个张量第0个指标为左虚拟指标，最后一个指标为右虚拟指标
    psi = tensors[0]
    for n in range(1, len(tensors)):
        psi = tc.tensordot(psi, tensors[n], [[-1], [0]])
    if psi.shape[0] > 1:  # 周期边界
        psi = psi.permute([0, psi.ndimension()-1] + list(range(1, psi.ndimension()-1)))
        s = psi.shape
        psi = tc.einsum('aab->b', psi.reshape(s[0], s[1], -1))
        psi = psi.reshape(s[2:])
    else:
        psi = psi.squeeze()
    return psi
x2 = full_tensor(tensors)
err = (x - x2).norm() / x.norm()
print('全局张量TTD（指标正序）误差 = %g' % err)

全局张量TTD（指标正序）误差 = 4.84283e-15

2.2 正交三角（QR）TT分解

这里我们也可以采用QR分解法

转载来源https://zhuanlan.zhihu.com/p/362248020

2.2.1 正交三角（QR）分解的定义

设 \pmb{A}_{m \times n} 的秩为 n ，则\pmb{A} 可以唯一地分解为

\pmb{A}_{m \times n} = \pmb{Q}_{m \times n} \pmb{R}_{n \times n} \\\\

其中，\pmb{Q}_{m \times n} 是标准正交向量组矩阵， \pmb{R}_{n \times n} 是正线上三角阵。

（补充一个小知识：\pmb{Q}其实是源于 orthogonal matrices 或 orthonormal basis，为了避免 \pmb{O},\pmb{0}不好区分的问题； \pmb{R}是指代 right triangular matrices）

2.2.2 正交三角（QR）分解的求法

其实，我们可以直接通过\pmb{Q}^T\pmb{A} = \pmb{R} 得出 \pmb{R}（因为有性质c： \pmb{Q}^T\pmb{Q}= \pmb{E} ，所以\pmb{Q}^T\pmb{A} = \pmb{Q}^T(\pmb{Q}\pmb{R}) = \pmb{E}\pmb{R} = \pmb{R}

综上，得出求解 \pmb{A}_{m \times n} 的正交三角（QR）分解\pmb{A}_{m \times n} = \pmb{Q}_{m \times n}\pmb{R}_{n \times n}的步骤：

第一步：对矩阵\pmb{A}_{m \times n}进行施密特标准正交化，得出矩阵\pmb{Q}_{m \times n} 。

第二步：通过 \pmb{R}_{n \times n} = \pmb{Q}_{m \times n}^T \pmb{A}_{m \times n} 得出矩阵\pmb{R}_{n \times n} 。

2.2.3 例子

求 \pmb{A}_{4 \times 3} 的正交三角（QR）分解，其中

\begin{aligned} \pmb{A}_{4 \times 3} = \begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} \end{aligned} \\\\ 

解：

第一步：对矩阵\pmb{A}_{m \times n}进行施密特标准正交化，得出矩阵\pmb{Q}_{m \times n} 。

对 \pmb{A}_{4 \times 3} 进行正交化，得：

\begin{aligned} \pmb{v}_1 = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix}, \pmb{v}_2 = \begin{bmatrix} -3 \\ 1 \\ 1 \\ 1 \end{bmatrix}, \pmb{v}_3 = \begin{bmatrix} 0 \\ -2/3 \\ 1/3 \\ 1/3 \end{bmatrix} \end{aligned} \\\\

单位化，得：

\begin{aligned} \pmb{Q}_{4 \times 3} = \begin{bmatrix} 1/2 & -3/\sqrt{12} & 0\\ 1/2 & 1/\sqrt{12} & -2/\sqrt{6} \\ 1/2 & 1/\sqrt{12} & 1/\sqrt{6} \\ 1/2 & 1/\sqrt{12} & 1/\sqrt{6} \end{bmatrix} \end{aligned} \\\\ 

第二步：通过\pmb{R}_{n \times n} = \pmb{Q}_{m \times n}^T \pmb{A}_{m \times n}得出矩阵 \pmb{R}_{n \times n} 。

\begin{aligned} \pmb{R}_{3 \times 3} &= \pmb{Q}_{4 \times 3}^T \pmb{A}_{4 \times3} \\\\ &= \begin{bmatrix} 1/2 & 1/2 & 1/2 & 1/2\\ -3/\sqrt{12} & 1/\sqrt{12} & 1/\sqrt{12} & 1/\sqrt{12} \\ 0 & -2/\sqrt{16} & 1/\sqrt{6} & 1/\sqrt{6} \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{bmatrix} \\\\ & = \begin{bmatrix} 2 & 3/2 & 1 \\ 0 & 3/\sqrt{12} & 2/\sqrt{12} \\ 0 & 0 & 2/\sqrt{6} \end{bmatrix} \end{aligned} \\\\

**解毕。

求 \pmb{A}_{5 \times 3} 的正交三角（QR）分解，其中

\begin{aligned} \pmb{A}_{5 \times 3} = \begin{bmatrix} 1 & 2 & 5 \\ -1 & 1 & -4 \\ -1 & 4 & -3 \\ 1 & -4 & 7 \\ 1 & 2 & 1 \end{bmatrix} \end{aligned} \\\\

解：

第一步：对矩阵\pmb{A}_{m \times n} 进行施密特标准正交化，得出矩阵\pmb{Q}_{m \times n} 。

对\pmb{A}_{5 \times 3}进行正交化，得：

\begin{aligned} \pmb{v}_1 = \begin{bmatrix} 1 \\ -1 \\ -1 \\ 1\\ 1 \end{bmatrix} , \pmb{v}_2 = \begin{bmatrix} 3 \\ 0 \\ 3 \\ -3\\ 3 \end{bmatrix}, \pmb{v}_3 = \begin{bmatrix} 2 \\ 0 \\ 2 \\ 2\\ -2 \end{bmatrix} \end{aligned} \\\\ 

单位化，得：

\begin{aligned} \pmb{Q}_{5 \times 3} = \begin{bmatrix} 1/\sqrt{5} & 1/2 & 1/2 \\ -1/\sqrt{5} & 0 & 0 \\ -1/\sqrt{5} & 1/2 & 1/2 \\ 1/\sqrt{5} & -1/2 & 1/2 \\ 1/\sqrt{5} & 1/2 & -1/2 \end{bmatrix} \end{aligned} \\\\ 

第二步：通过\pmb{R}_{n \times n} = \pmb{Q}_{m \times n}^T \pmb{A}_{m \times n} 得出矩阵 \pmb{R}_{n \times n}。

\begin{aligned} \pmb{R}_{3 \times 3} &= \pmb{Q}_{5 \times 3}^T \pmb{A}_{5 \times3} \\\\ &= \begin{bmatrix} 1/\sqrt{5} & -1/\sqrt{5} & -1/\sqrt{5} & 1/\sqrt{5} & 1/\sqrt{5} \\ 1/2 & 0 & 1/2 & -1/2 & 1/2 \\ 1/2 & 0 & 1/2 & 1/2 & -1/2 \end{bmatrix} \begin{bmatrix} 1 & 2 & 5 \\ -1 & 1 & -4 \\ -1 & 4 & -3 \\ 1 & -4 & 7 \\ 1 & 2 & 1 \end{bmatrix} \\\\ & = \begin{bmatrix} \sqrt{5} & -\sqrt{5} & 4\sqrt{5} \\ 0 & 6 & -2 \\ 0 & 0 & 4 \end{bmatrix} \end{aligned} \\\\